
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Моделі стаціонарних випадкових процесів із дискретним часом
|
|
Випадкові процеси з дискретним часом належать до множини часових рядів, тобто впорядковані по часу і являють собою скінченні або зліченні послідовності випадкових величин (більш докладне означення часового ряду наведено в наступному підрозділі 4.3). Така модель широко використовується для опису сигналів при вирішенні різноманітних прикладних задач.
Використання засобів обчислювальної техніки при аналізі сигналів пов’язано з перетворенням неперервних сигналів в сигнали з дискретним часом, що знову приводить до розгляду часових рядів.
На сьогодні розроблені ймовірнісні і статистичні методи аналізу часових рядів. Класичні результати аналізу приведені в роботах Т.В.Андерсона (T.W.Anderson), М.С.Бартлета (M.S.Bartlett), У.Гренандера (U.Grenander), Дж.Дуба (J.L.Doob), А.М.Колмогорова, Г.Крамера (H.Cramer), М.Розенблата (M.Rosenblatt), Е.Хеннена (E.J.Hannan) та інших.
В цьому підрозділі коротко зупинимось на результатах аналізу стаціонарних процесів з дискретним часом. Для слабо стаціонарного процесу з дискретним часом має місце теорема Герглотца (G.Herglotz, 1911р.).
ТЕОРЕМА ГЕРГЛОТЦА. Для довільної дійсної стаціонарної послідовності  функція
функція 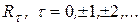 може бути представлена у вигляді
може бути представлена у вигляді
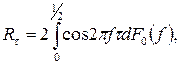 (4.6)
(4.6)
де  дійсна, неперервна зліва, неспадна функція на відрізку
дійсна, неперервна зліва, неспадна функція на відрізку  , для якої
, для якої 
Зауважимо, що при цьому
 (4.7)
(4.7)
Ця теорема є аналогом теореми Хінчина для процесів з неперервним часом. Наведемо дещо змінене формулювання теореми Герглотца для дійсного процесу, в формі, яка буде зручною для пояснення наступних викладок. При цьому функції  та
та  набувають іншого змісту, який буде зберігатися на протязі всього подальшого матеріалу.
набувають іншого змісту, який буде зберігатися на протязі всього подальшого матеріалу.
ТЕОРЕМА. Якщо  - дійсний, слабо стаціонарний випадковий процес з
- дійсний, слабо стаціонарний випадковий процес з 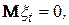 то його кореляційна функція може бути представлена у вигляді
то його кореляційна функція може бути представлена у вигляді
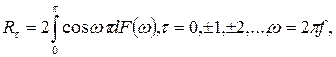 (4.8)
(4.8)
де 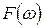 - називається спектральною функцією процесу і визначається за допомогою співвідношення
- називається спектральною функцією процесу і визначається за допомогою співвідношення
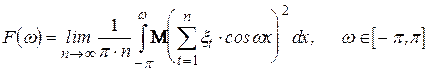 . (4.9)
. (4.9)
У випадку, коли відомі значення  спектральна функція
спектральна функція 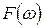 визначається за допомогою ряду Фур'є-Стілтьєса. Враховуючи (4.9), можна записати
визначається за допомогою ряду Фур'є-Стілтьєса. Враховуючи (4.9), можна записати
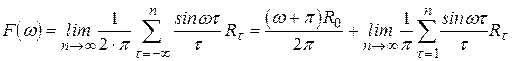 , (4.10)
, (4.10)
зауваживши при цьому, що формула (4.8) в загальному випадку дозволяє визначити коефіцієнти Фур'є-Стілтьєса цього ряду. Це означає, що при  потрібно взяти доданок
потрібно взяти доданок 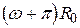 .
.
Відзначимо, що вимога 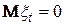 потрібна для забезпечення співвідношення (4.9). Спектральна функція задає спектральну міру на колі. Спектральна функція
потрібна для забезпечення співвідношення (4.9). Спектральна функція задає спектральну міру на колі. Спектральна функція 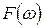 є дійсна, неспадна і може змінюватися як неперервно так і стрибками і на відміну від раніше введених спектральних функцій, тут відсутнє нормування та допускаються не нульові значення при
є дійсна, неспадна і може змінюватися як неперервно так і стрибками і на відміну від раніше введених спектральних функцій, тут відсутнє нормування та допускаються не нульові значення при 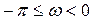 , тобто повна зміна
, тобто повна зміна 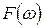 на інтервалі
на інтервалі 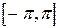 дорівнює
дорівнює  , де
, де 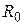 - дисперсія або середня потужність процесу
- дисперсія або середня потужність процесу  , а
, а 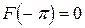 . Із співвідношення (4.9) зразу випливає, що
. Із співвідношення (4.9) зразу випливає, що 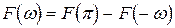 при всіх
при всіх 
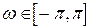 , тому
, тому 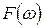 повністю визначається своїми значеннями на інтервалі
повністю визначається своїми значеннями на інтервалі 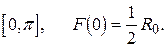
Якщо існує абсолютно неперервна функція 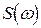 , така, що
, така, що


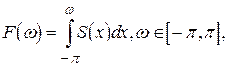 (4.11)
(4.11)
то 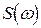 називають спектральною щільністю потужності процесу
називають спектральною щільністю потужності процесу  з дискретним часом. Для дійсного процесу
з дискретним часом. Для дійсного процесу 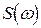 дійсна і
дійсна і 
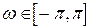 .
.
Формула (4.8), при умові, що існує 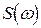 , визначає коефіцієнти ряду Фур'є для спектральної щільності, тому
, визначає коефіцієнти ряду Фур'є для спектральної щільності, тому 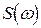 можна зобразити рядом Фур'є у вигляді
можна зобразити рядом Фур'є у вигляді

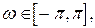 (4.12)
(4.12)