Спектральні оцінки часового ряду. Періодограма

Нехай спостерігається 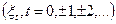- дійсний гільбертів слабо стаціонарний процес із заданим кінцевим математичним сподіванням . Передбачається, що для даного процесу існує невідома спектральна щільність потужності і виконується ергодична теорема відносно математичного сподівання і кореляційної функції (умова сильного перемішування).

Як і у попередньому випадку оцінювання кореляційної функції, тут також спостерігається послідовність – реалізація вихідного процесу 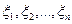. В якості оцінки 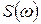можна взяти

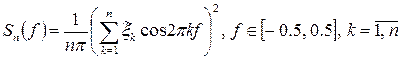, (5.12)

де .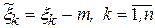

Вираз (5.12) можна записати у вигляді

.

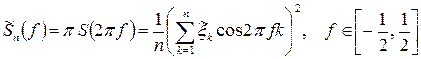Якщо відліки взяти не через одиницю часу, а з довільним постійним кроком , то останній вираз можна записати так

.

Частота 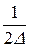- найвища частота, яку можна виявити за даними відліку через 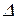секунд – частота Найквіста – Котельнікова.

Приведений вище вигляд оцінки спектральної щільності можна пояснити таким чином. Якщо вважати значення 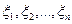коефіцієнтами відрізку ряду Фур'є, то 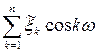є періодичною функцією від 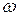, задану на періоді , яка в цей ряд розкладена. А оскільки 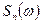– оцінка спектральної щільності потужності, то наведена вище сума в оцінці (5.12) береться в квадраті умножається на .

Функцію 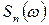в статистичній теорії спектральних функцій називають періодограмою. Її вперше ввів і досліджував в своїх роботах Шастер в 1898 р. і 1906 р. Якщо вихідний процес 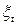– гаусів, то періодо­грама 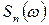, 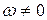і 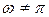, розподілена, як 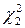– хі - квадрат з двома ступінями свободи.

Приведемо без доказу математичне сподівання оцінки (5.12) при 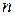, що прямує до нескінченності

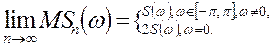
Останнє співвідношення показує, що при 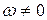оцінка 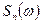є асимптотично не­зміщеною для

.

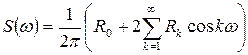Обчислення дисперсії 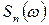в загальному випадку зв'язане із складними викладеннями, які спрощуються в разі аналізу гаусових процесів 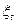. Приведемо без доказу асимптотичне значення дисперсії 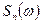у гаусовому випадку