
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кореляція
|
|
Слід відмітити той факт, що найкраще наближення обраної для апроксимації прямої (або кривій) до експериментальних даних зовсім не означає, що реально існуюча фізична залежність щонайкраще описується апроксимуючим рівнянням, відповідним саме цієї лінії. Математичні операції завжди лише наводять до значень параметрів, що забезпечують найкраще (у сенсі критерію найменших квадратів) наближення до рівняння вибраного вигляду. Наочний цьому приклад наведено рис. 6.5: тут можна бачити, що одержані експериментальні дані зовсім не відповідають лінійній залежності, хоча пряма підібрана так, що забезпечує найкраще наближення до цих даних.
Для оцінки того, наскільки добре обрана пряма (і відповідне їй рівняння) насправді узгоджується з експериментальними даними, необхідно практично використати кореляційні методи, математичний апарат яких було розглянуто у попередніх лекціях. Кореляційні методи надають можливість судити про те, наскільки тісно улягаються експериментальні точки на апроксимуючу криву. Якщо регресія визначає передбачуване співвідношення між змінними, то кореляція показує, наскільки добре це

Рис. 6.5
співвідношення відображує дійсність. Сильна кореляція між змінними означає, що ці зміни взаємозв'язані (рис. 6.6), проте необхідно мати на увазі, що це ще не доводить наявність причинно-наслідкового зв'язку між змінними. При регресійному аналізі передбачається наявність причинно-наслідкового зв'язку між залежною і незалежною змінними: при кореляційному аналізі таке допущення не робиться.
Часто розповідають історію, що про одному державному діячі, який виявив, що в його державі є вельми сильна кореляція між зростанням продажу пива і збільшенням доходів шкільних вчителів. Звідси він зробив вивід, що немає сенсу підвищувати вчителям зарплату, оскільки вони почнуть споживати більше пива. Ймовірно, він міг би виявити настільки ж сильну кореляцію між зростанням зарплати вчителів і ростом злочинності, числа незаконнонароджених і інфляції. Фактично він міг би знайти сильну кореляцію і зв'язати регресійною кривою будь-які два явища, які зростають більш менш однаковим чином.
У цьому жартівливому прикладі істотне те, що аналітик прийняв допущення (гіпотезу) про наявність причинно-наслідкового зв'язку між явищами, яке робиться при регресійному аналізі. Але в даному випадку це допущення може і не бути правильним. Кореляція говорить лише про те, наскільки тісно експериментальні точки лягають на апроксимуючу криву. Але вона не може сказати, чи справедливе основне допущення про наявність причинно-наслідкового зв'язку. Кореляційний аналіз показує лише ступінь відповідності одержаних даних гіпотезі, що прийнято.
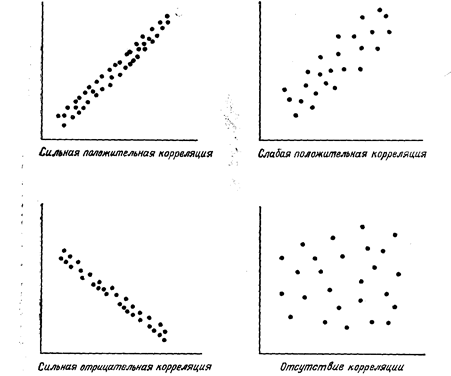
Рис. 6.6
Коефіцієнт кореляції лежить в межах від — 1 до + 1. Коефіцієнт — 1 відповідає максимальною негативній кореляції, коли 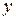 зменшується із збільшенням
зменшується із збільшенням  , а всі експериментальні точки лежать точно на кривій. Коефіцієнт 0 свідчить про повну відсутність кореляції, а коефіцієнт + 1 — відповідає максимальній позитивній кореляції. Всі ці крайні випадки зустрічаються дуже і дуже рідко; зазвичай коефіцієнт кореляції має деяке дробове значення, і його ще слід перевіряти на статистичну значущість.
, а всі експериментальні точки лежать точно на кривій. Коефіцієнт 0 свідчить про повну відсутність кореляції, а коефіцієнт + 1 — відповідає максимальній позитивній кореляції. Всі ці крайні випадки зустрічаються дуже і дуже рідко; зазвичай коефіцієнт кореляції має деяке дробове значення, і його ще слід перевіряти на статистичну значущість.
Для випадку простої лінійної регресійної задачі (тобто для випадку, коли є одна залежна і одна незалежна змінні, зв'язані між собою лінійно) коефіцієнт кореляції  обчислюється за формулою
обчислюється за формулою
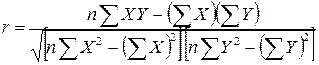 (6.4)
(6.4)
Практичне застосування наведеної формули розглянемо на конкретному прикладі
ПРИКЛАД 6.2. Використовуючи дані з ПРИКЛАДУ 6.1, обчислимо коефіцієнт кореляції  , як це показано в таблиці 6.2. У відповідності з формулою (6.4), маємо
, як це показано в таблиці 6.2. У відповідності з формулою (6.4), маємо
 .
.
Таблиця 6.2
| X | Y | XY | Х2 | Y2 |
| 0 | 0 | |||
| Суммы 7 |
Загальний розкид 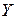 визначається як
визначається як 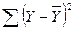 , тобто рівний сумі квадратів відхилень
, тобто рівний сумі квадратів відхилень 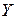 від середнього значення
від середнього значення 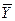 . Відношення цієї величини розкиду, що обумовлюється запропонованим регресійним рівнянням, до загального спостережуваного розкиду називається коефіцієнтом детермінації і рівно квадрату коефіцієнту кореляції. Таким чином, для наведеного прикладу, в якому ми обчислили
. Відношення цієї величини розкиду, що обумовлюється запропонованим регресійним рівнянням, до загального спостережуваного розкиду називається коефіцієнтом детермінації і рівно квадрату коефіцієнту кореляції. Таким чином, для наведеного прикладу, в якому ми обчислили  = 0, 969, коефіцієнт детермінації
= 0, 969, коефіцієнт детермінації  . Це означає, що в 93, 9% випадків відхилення
. Це означає, що в 93, 9% випадків відхилення 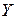 при змінах
при змінах 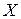 відповідає наведеному рівнянню.
відповідає наведеному рівнянню.
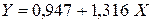 .
.
Контрольні запитання
1. Пояснити практичну суть застосування методу підбору апроксимуючих кривих.
2. Які задачі вирішують методи регресійного та кореляційного аналізу при проведенні апроксимації експериментальних даних?
3. Назвати послідовність кроків при підборі кривої під час проведення апроксимації.
4. Які основні типи кривих використовують при проведенні апроксимації?
5. Пояснити основну ідею застосування методу найменших квадратів.
6. Дати узагальнене означення регресійного аналізу.
7. Навести основне рівняння моделі лінійної регресії.
8. Записати основні співвідношення для визначення коефіцієнтів регресії.
9. Пояснити, які основні задачі вирішуються кореляційними методами при проведенні апроксимації?
10. Що характеризує коефіцієнт кореляції при аналізі експериментальних даних?
11. Навести приклади графічних залежностей експериментальних даних, що відповідають:
а) сильній позитивній кореляції;
б) сильній негативній кореляції;
в) слабкій позитивній кореляції;
г) повній відсутності кореляції.