
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерій Колмогорова — Смирнова
|
|
Ще один широко використовуваний критерій для статистичної перевірки гіпотез був запропонований Смирновим в 1939 р. і в подальшому розвинений самим автором і Колмогоровим.
Він застосовується в тих випадках, коли розподіл, що перевіряється, безперервний і відомі середнє і дисперсія досліджуваної сукупності. Таблиця його критичних значень була опублікована Смирновим в 1948 р. і багато разів перевидавалася. Подібно до критерію  критерій Колмогорова — Смирнова може бути використаний для перевірки відповідності між розподілом сукупності емпіричних даних і деяким конкретним теоретичним розподілом. Перевірка здійснюється шляхом завдання інтегральної функції, яка витікає з теоретичного розподілу, і її порівняння з інтегральною функцією розподілу емпіричних даних.
критерій Колмогорова — Смирнова може бути використаний для перевірки відповідності між розподілом сукупності емпіричних даних і деяким конкретним теоретичним розподілом. Перевірка здійснюється шляхом завдання інтегральної функції, яка витікає з теоретичного розподілу, і її порівняння з інтегральною функцією розподілу емпіричних даних.
Порівняння ґрунтується на вибірковій групі, в якій експериментальний розподіл має найбільше абсолютне відхилення від теоретичного. Далі ця абсолютна різниця порівнюється з критичними значеннями (див. додаток В.2 [4]) з метою визначення, чи може таке відхилення бути випадковим при даному законі розподілу.
ПРИКЛАД 7.3. Для ілюстрації візьмемо дані таблиці 7.2, які вже перевіряли по критерію  на відповідність розподілу Пуассона (приклад 7.1). Раніше для цієї сукупності даних було обчислено
на відповідність розподілу Пуассона (приклад 7.1). Раніше для цієї сукупності даних було обчислено 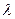 = 0, 5577. Гіпотеза Н0 полягає в тому, що немає суттєвих відмінностей між спостережуваними даними і тими, які повинні одержуватись в разі розподілу Пуассона, з середнім значенням 0, 5577 і n = 509. Перш за все необхідно отримати два інтегральних розподілу — із спостережуваних даних і з теоретичного розподілу — и знайти абсолютні різниці для всіх груп значення випадкової величини. Це виконано в таблиці 7.7.
= 0, 5577. Гіпотеза Н0 полягає в тому, що немає суттєвих відмінностей між спостережуваними даними і тими, які повинні одержуватись в разі розподілу Пуассона, з середнім значенням 0, 5577 і n = 509. Перш за все необхідно отримати два інтегральних розподілу — із спостережуваних даних і з теоретичного розподілу — и знайти абсолютні різниці для всіх груп значення випадкової величини. Це виконано в таблиці 7.7.
Таблиця 7.7