
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ідентифікація закону розподілу
|
|
Ідентифікація закону розподілу за експериментальними даними
Ідентифікація закону розподілу. Оцінка розподілу по критеріям згоди " хі - квадрат" та Колмогорова - Смірнова.
Ідентифікація закону розподілу
Якщо деякі з елементів системи поводяться стохастично, то в процесі звичайного моделювання виникає проблема: як перевірити сумісність експериментальних даних з деяким теоретичним розподілом? Інакше кажучи, виникає питання: чи відповідає частота спостережуваних вибіркових значень тій частоті, з якою вони повинні б появляться при деякому імовірнісному розподілі, що відповідає певному теоретичному закону? Якщо частота подій (значень вимірюваної величини) близька до величини, що передбачається теоретично, то надалі можна будувати модель вихідних або очікуваних подій на основі теоретичного розподілу.
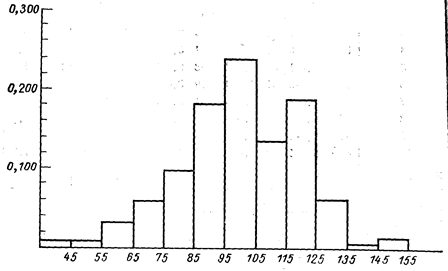
Рис. 7.1. Гістограма для даних табл. 7.1
Зазвичай, при проведенні експерименту одразу не можна висловити розумну здогадку (гіпотезу) відносно розподілу випадкової змінної, поки не зберемо і не проаналізуємо достатню кількість об'єктивних (облікових або експериментальних) даних, що відносяться до досліджуваного експерименту. Зібрані дані зазвичай підсумовують у вигляді розподілу відносних частот (гістограми, див. лекцію 5); така гістограма приведена на рис. 7.1. Якщо маємо справу з дискретною змінною, то записуємо частоти появи кожного з її можливих значений. Якщо змінна безперервна, розбиваємо весь діапазон її значень на рівні інтервали (групи) і записуємо частоти появи кожної групи. Число груп зазвичай беруть в межах від 5 до 20 залежно від конкретних даних. Тоді відносна частота для кожної групи дорівнює частки від ділення спостережуваного числа події даної групи на загальне число подій. Таблиця 7.1 і рис. 7.1 ілюструють порядок такої обробки експериментальних даних при неперервній змінній, а таблиця. 7.2 і рис. 7.2 — при дискретній.
Таблиця 7.1
Розподіл тижневої продуктивності
| Тижнева продуктивність (х) | Частота | P(x) |
| Менше 46 | 0, 008 | |
| 46—55 | 0, 008 | |
| 56—65 | 0, 025 | |
| 66—75 | 0, 058 | |
| 76—85 | 0.092 | |
| 86—95 | 0, 175 | |
| 96—105 | 0, 234 | |
| 106—115 | 0, 134 | |
| 116—125 | 0, 183 | |
| 126—135 | 0, 058 | |
| 136—145 | 0, 008 | |
| 146 і вище | 0, 017 | |
 120 120
|  1, 000 1, 000
|
Закінчивши побудову гістограми, зазвичай переходять до підбору відповідного до даного випадку теоретичного закону розподілу. Перший спосіб — візуально порівняти отриману гістограму з декількома кривими теоретичних розподілів. Так, порівнюючи гістограму рис. 7.2 з теоретичними кривими, приведеними на рис. 7.3, можна бачити, що вона схожа на розподіл Пуассона. В той же час гістограма рис. 7.1 схожа з кривою нормального розподілу. Проте таке візуальне порівняння дозволяє лише передбачити, до якого теоретичного розподілу треба прагнути «підігнати» експериментальне, і ніколи не дає достатніх підстав, аби остаточно прийняти деяку гіпотезу (теоретичний розподіл).
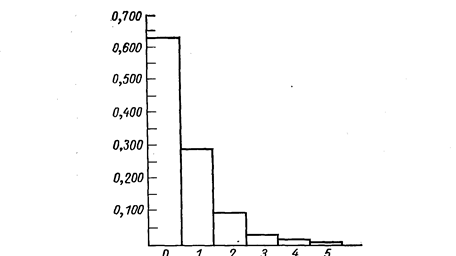
Рис. 7.2. Гістограма для відносних частот даних табл. 7.2
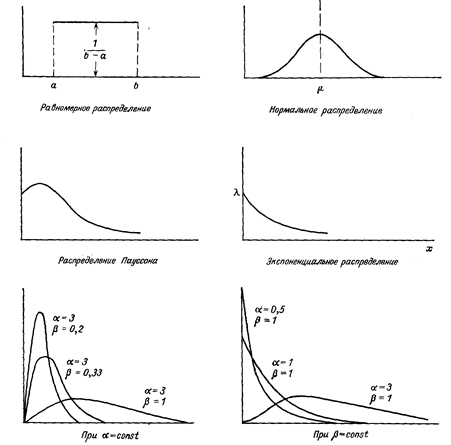
Рис. 7.3. Типові теоретичні криві розподілу ймовірностей
Після того, як аналітично підібрано одне або декілька теоретичних розподілів (наприклад, нормальне, Пуассона, біноміальне, гамма-розподіл і т. д.), з якими, як передбачається, можна погоджувати експериментальні дані, слід визначити параметри розподілу, з тим аби піддати їх перевірці за допомогою статистичних критеріїв. Якщо передбачуваний розподіл є функцією двох параметрів, останні зазвичай удається оцінити на основі вибіркового середнього і вибіркової дисперсії.
Таблиця 7.2
Розподіл відносних частот телефонних запитів за одночасовий інтервал
| Число запитів N | Число одночасових інтервалів с N запитами | Відносна частота |
| 0, 619 | ||
| 0, 279 | ||
| 0, 078 | ||
| 0, 018 | ||
| 0, 004 | ||
| 0, 002 | ||
 509 509
|  1, 000 1, 000
|
Коли експериментальні дані розбиті на групи, середнє і дисперсію можна обчислити за відповідними формулами
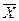
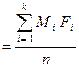 ,
,
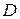 =
= 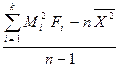 ,
,
де 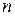 — повний об'єм вибірки,
— повний об'єм вибірки, 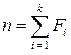 ;
;
k — число груп (інтервалів вибірки);
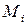 —середня точка i - гo інтервалу або (для дискретних даних) значення i - ой групи;
—середня точка i - гo інтервалу або (для дискретних даних) значення i - ой групи;
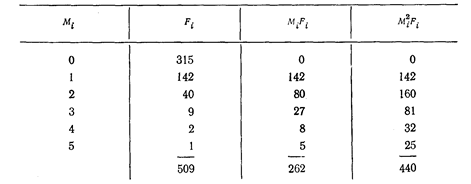
Таблиця 7.3
Обчислення статистичних параметрів для дискретних даних табл. 7.2
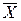
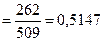
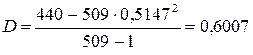
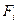 — частота появлення
— частота появлення 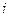 - ої групи або
- ої групи або 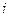 -гo інтервалу.
-гo інтервалу.
Для дискретних даних таблиці 7.2 необхідні обчислення зведено в таблицю 7.3, а для неперервних даних таблиці 7.1 — в таблицю 7.4.
Спочатку було зроблено припущення, що даним таблицям. 7.2 може відповідати розподіл Пуассона. Із [1,..., 3] відомо, що в цьому розподілі середнє дорівнює дисперсії (зазвичай позначається 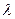 ), а з таблиці 7.3 видно, що для експериментальних даних середнє не дорівнює дисперсії: 0, 5147< 0, 6007. Це могло б змусити нас відкинути гіпотезу про те, що експериментальний розподіл - пуассонівський. Проте в даному конкретному випадку маємо як практичні, так і теоретичні підстави не відмовлятися від цієї гіпотези. Коли вірогідність деякої події для одного тимчасового інтервалу така ж, як для будь-якого іншого, а здійснення якої-небудь події не робить впливу на ймовірність його повторної появи, є вагома підстава чекати розподіл Пуассона. Додаткові підстави для цього отримуємо, якщо в будь-якому інтервалі часу має місце висока вірогідність появи нульового числа подій і якщо середнє число подій в кожному тимчасовому інтервалі мало.
), а з таблиці 7.3 видно, що для експериментальних даних середнє не дорівнює дисперсії: 0, 5147< 0, 6007. Це могло б змусити нас відкинути гіпотезу про те, що експериментальний розподіл - пуассонівський. Проте в даному конкретному випадку маємо як практичні, так і теоретичні підстави не відмовлятися від цієї гіпотези. Коли вірогідність деякої події для одного тимчасового інтервалу така ж, як для будь-якого іншого, а здійснення якої-небудь події не робить впливу на ймовірність його повторної появи, є вагома підстава чекати розподіл Пуассона. Додаткові підстави для цього отримуємо, якщо в будь-якому інтервалі часу має місце висока вірогідність появи нульового числа подій і якщо середнє число подій в кожному тимчасовому інтервалі мало.
Таблиця 7.4
Обчислення статистичних параметрів для неперервних даних табл. 7.1
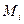
| 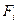
| 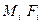
| 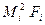
|
| 40, 5 | 40, 5 | 1640, 25 | |
| 50, 5 | 50, 5 | 2550, 25 | |
| 60, 5 | 181, 5 | 10980, 75 | |
| 70, 5 | 493, 5 | 34791, 75 | |
| 80, 5 | 885, 5 | 71282, 75 | |
| 90, 5 | 1900, 5 | 171995, 25 | |
| 100, 5 | 2814, 0 | 282807, 00 | |
| 110, 5 | 1768, 0 | 195364, 00' | |
| 120, 5 | 2651, 0 | 319445, 50' | |
| 130, 5 | 913, 5 | 119211, 75 | |
| 140, 5 | 140, 5 | 19740, 25 | |
| 150, 5 | 301, 0 | 45300, 50 | |
| 12140, 0 | 1275110, 00 |
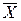
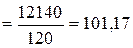
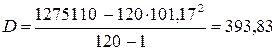
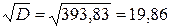
У наведеному прикладі дані таблиці 7.2, що представляють число запитів, що отримуються по телефону в бюро технічної інформації, задовольняють всім цим критеріям. Якщо хочемо і далі вважати можливим розподіл Пуассона, то можна прийняти, що 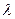 дорівнює середній величині між вибірковим середнім і вибірковою дисперсією, тобто
дорівнює середній величині між вибірковим середнім і вибірковою дисперсією, тобто
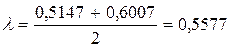
6.2. Оцінка розподілу за критерієм згоди «хі - квадрат»
Для статистичної оцінки гіпотези про те, що сукупність емпіричних, або вибіркових, даних трохи відрізняється від тієї, яку можна чекати при деякому теоретичному законі розподілу, розглянемо два види випробувань на відповідність зробленій гіпотезі. Одним з параметрів, що дозволяють оцінити розходження між спостережуваними і очікуваними частотами, є величина  (слід читати «хі - квадрат»). Критерій «хі - квадрат» був запропонований Пірсоном в 1903 р., хоча повністю цей метод був розроблений Фішером, що опублікував в 1924 р. відповідні таблиці критичних величин, які практично застосовуються і на даний час. Статистика визначається виразом
(слід читати «хі - квадрат»). Критерій «хі - квадрат» був запропонований Пірсоном в 1903 р., хоча повністю цей метод був розроблений Фішером, що опублікував в 1924 р. відповідні таблиці критичних величин, які практично застосовуються і на даний час. Статистика визначається виразом
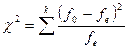
де 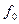 — спостережувана частота для кожної групи або інтервалу;
— спостережувана частота для кожної групи або інтервалу;
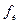 — очікувана частота для кожної групи або інтервалу;
— очікувана частота для кожної групи або інтервалу;
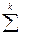 — передбачена теоретичним розподілом сума по всім групам або
— передбачена теоретичним розподілом сума по всім групам або
інтервалам.
Якщо 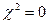 , то спостережувані і теоретично передбачені значення частот точно збігаються; якщо ж
, то спостережувані і теоретично передбачені значення частот точно збігаються; якщо ж  > 0, то повною збіжності немає. Чим більше величина
> 0, то повною збіжності немає. Чим більше величина  , тим більше розбіжність між спостережуваними і очікуваними значеннями. Якщо
, тим більше розбіжність між спостережуваними і очікуваними значеннями. Якщо 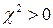 , то необхідно порівняти розрахункові значення з табличними (наприклад, додаток В.3, [4]) для того, щоб оцінити, наскільки спостережувані значення визначаються лише випадковими причинами. Значення статистики
, то необхідно порівняти розрахункові значення з табличними (наприклад, додаток В.3, [4]) для того, щоб оцінити, наскільки спостережувані значення визначаються лише випадковими причинами. Значення статистики  табульовані для різних чисел ступнів свободи і різних рівнів довірчої вірогідності 1 —
табульовані для різних чисел ступнів свободи і різних рівнів довірчої вірогідності 1 — 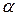 . При практичному використанні цієї статистики припускається так звана нульова гіпотеза Н0 про те, що між спостережуваним і очікуваним теоретичним розподілом з тими ж параметрами немає значних розбіжностей. Якщо при перевірці цієї гіпотези розрахункова величина
. При практичному використанні цієї статистики припускається так звана нульова гіпотеза Н0 про те, що між спостережуваним і очікуваним теоретичним розподілом з тими ж параметрами немає значних розбіжностей. Якщо при перевірці цієї гіпотези розрахункова величина  виявляється більше критичного табличного значення (для даного рівня довірчої вірогідності і відповідного числа ступнів свободи), то можна укласти, що при даному рівні довірчої ймовірності спостережувані частоти значно відрізняються від очікуваних, і тоді слід було б відкинути гіпотезу Н0.
виявляється більше критичного табличного значення (для даного рівня довірчої вірогідності і відповідного числа ступнів свободи), то можна укласти, що при даному рівні довірчої ймовірності спостережувані частоти значно відрізняються від очікуваних, і тоді слід було б відкинути гіпотезу Н0.
Застосовуючи метод перевірки гіпотез по критерію згоди  , слід пам'ятати наступне:
, слід пам'ятати наступне:
1. Відносні значення частот або їх значення, виражені у відсотках, брати не можна; іншими словами, необхідно користуватись даними прямих спостережень або абсолютними значеннями частот.
2. Значення спостережуваних частот для кожної групи або інтервалу мають дорівнювати 5 або більш. Якщо це не так, то суміжні групи або інтервали повинні об'єднуватися.
3. Число рівнів свободи задається вираженням 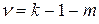 , де
, де 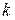 —число груп або інтервалів і
—число груп або інтервалів і 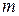 — число параметрів, що визначаються дослідним шляхом або на основі вибіркових даних для обчислення очікуваних значень частот.
— число параметрів, що визначаються дослідним шляхом або на основі вибіркових даних для обчислення очікуваних значень частот.
Розглянемо два приклади з практичного застосування критерію 
ПРИКЛАД 7.1. Припустимо, що необхідно перевірити дані таблиці 7.2. на їх відповідність розподілу Пуассона при довірчому рівні 0, 95. Відомо
[1, …, 3], що розподіл Пуассона виражається формулою
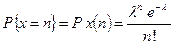
де 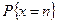 — вірогідність настання
— вірогідність настання 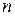 подій;
подій; 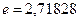 ;
;
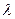 — позитивна константа (яка одночасно є і середнім значенням, і дисперсією).
— позитивна константа (яка одночасно є і середнім значенням, і дисперсією).
У попередньому підрозділі було визначено, що для випадку, який розглядається 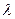 = 0, 5577; тому гіпотеза Н0 формулюється наступним чином: немає істотних відмінностей між спостережуваними даними і даними, які виходять з розподілу Пуассона з математичним сподіванням, або середнім
= 0, 5577; тому гіпотеза Н0 формулюється наступним чином: немає істотних відмінностей між спостережуваними даними і даними, які виходять з розподілу Пуассона з математичним сподіванням, або середнім 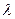 = 0, 5577. Узявши у формулі розподілу Пуассона це значення і потім підставив послідовно n = 0, n =1, n = 2 і т. д., отримаємо дані, представлені в таблиці 7.5.
= 0, 5577. Узявши у формулі розподілу Пуассона це значення і потім підставив послідовно n = 0, n =1, n = 2 і т. д., отримаємо дані, представлені в таблиці 7.5.
Таблиця 7.5
Розрахункові величини  для табл. 7.2
для табл. 7.2
| п | 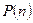
| 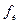
| 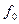
| 
|
| 0, 571 0, 319 0, 089 0, 017 0, 003 0, 001 | 1 11 | 2 12 | 1, 98 2, 47 0, 56 0, 09 | |
| 1, 000 | 5, 10 |
Для одержання 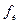 умножимо відповідну величину
умножимо відповідну величину 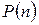 на 509. Розрахункова величина
на 509. Розрахункова величина  = 5, 10. Підшукуємо критичне значення величини з додатку В.3 [4] для довірчого рівня 0, 95 і числа ступнів свободи 4 - 1 - 1 = = 2, знаходимо
= 5, 10. Підшукуємо критичне значення величини з додатку В.3 [4] для довірчого рівня 0, 95 і числа ступнів свободи 4 - 1 - 1 = = 2, знаходимо  = 5, 99. Отже, оскільки розрахункова величина
= 5, 99. Отже, оскільки розрахункова величина  менше табличного критичного значення, гіпотезу Н0 не відкидаємо. Останні три групи значень в проведеному розрахунку були об'єднані з тим, аби набути значення частоти, принаймні рівного 5 в кожній групі; таким чином, замість початкових 6 груп ми отримали 4. Так само при визначенні числа ступнів свободи, було зменшено його на одиницю тому, що для розрахунку очікуваної частоти використовувалася величина
менше табличного критичного значення, гіпотезу Н0 не відкидаємо. Останні три групи значень в проведеному розрахунку були об'єднані з тим, аби набути значення частоти, принаймні рівного 5 в кожній групі; таким чином, замість початкових 6 груп ми отримали 4. Так само при визначенні числа ступнів свободи, було зменшено його на одиницю тому, що для розрахунку очікуваної частоти використовувалася величина 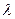 , отримана з даних спостереження.
, отримана з даних спостереження.
ПРИКЛАД 7.2. Припустимо, що розглядається вибірка, одержана з генератора випадкових чисел, який видав 500 цифр, розподілених по випадковому закону. Зареєстрована частота їх появи представлена в таблиці 7.6. Якби цифри генерувалися дійсно по випадковому закону, то можна було б чекати, що кожна цифра появиться близько 50 разів. Використовуючи рівень значущості 0, 99, перевіримо, наскільки отримані результати відповідають рівномірному розподілу. Хід розрахунків ілюструється таблицею 7.6.
Таблиця 7.6
Розрахунок величини  за даними прикладу 7.2
за даними прикладу 7.2
| Цифра | о | l | Всього | ||||||||
| Частоти, що спостерігаються | |||||||||||
| Очікувані частоти | |||||||||||

| 2, 88 | 1, 28 | 3, 92 | 9, 68 | 2, 00 | 8, 00 | 2, 00 | 2, 00 | 9, 68 | 5, 12 | 46, 56 |
Таблична величина  = 21, 7 для
= 21, 7 для 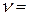 10 - 1= 9 і
10 - 1= 9 і 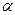 = 0, 01
= 0, 01
Оскільки 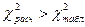 , гіпотеза Н0 відхиляється
, гіпотеза Н0 відхиляється