Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Електричні двополюсники
|
|
Математичні моделі простіших елементів
Математичні моделі простіших типових елементів, що утворюють технічні системи. Електричні двополюсники. Найпростіші елементи механічних систем
Математичні моделі простіших типових елементів, що утворюють технічні системи.
При всій різноманітності фізичних і технічних об'єктів, в яких набрякають процеси різної фізичної природи, зазвичай удається виділити окремі блоки, агрегати або вузли, кожен з яких залежно від перетворюваної фізичної субстанції можна розглядати як електричну, механічну поступальну або обертальну, теплову, гідравлічну або пневматичну систему [1]. У загальному випадку ці системи взаємозв'язані, але, використовуючи принцип декомпозиції, їх можна представити сукупністю простих типових елементів, що описуються порівняно нескладними математичними моделями макрорівня. Серед зовнішніх і вихідних параметрів, що характеризують стан кожного такого елементу, удається виділити величини, що мають сенс потенціалів і потоків фізичних субстанцій (наприклад, різниця електричних потенціалів і сила струму, різниця температур і тепловий потік і тому подібне). Ці величини називатимемо потенційними і потоковими відповідно. Зв'язок між цими величинами встановлюють за допомогою так званих рівнянь стану елементу, в які входять також і його внутрішні параметри.
Електричні двополюсники
Не дивлячись на відмінність фізичних процесів, що протікають в типових елементах всіляких технічних об'єктів, більшість цих елементів удається об'єднати в три групи, кожну з яких зручно охарактеризувати на прикладі так званих пасивних електричних двополюсників: резистора, конденсатора без втрат заряду і індуктивної котушки без опору. Резистор є характерним представником типового елементу, що має властивість чинити опір перенесенню деякій фізичною субстанції (в даному випадку — електричних зарядів). Для проходження через такий елемент потоку цієї субстанції необхідно створити різницю потенціалів на вході в елемент і виході з нього. Конденсатор володіє властивістю накопичувати цю субстанцію при підвищенні різниці потенціалів, а індуктивна котушка — властивістю інерції, що виявляється в прагненні зберегти потік цієї субстанції незмінним.
Виявляється, що серед простих типових елементів, в яких протікають процеси іншої фізичної природи в порівнянні з електричною системою, існують елементи з властивостями, аналогічними вказаним властивостям резистора, конденсатора і індуктивної котушки. Тому розгляд доцільно почати з рівнянь стану простих елементів електричної системи, а потім по аналогії з ними будувати математичні моделі (ММ) типових елементів, характерних для інших технічних систем.
У [1] відмічено, що ММ резистора, що описує протікання через нього електричного струму, є добре відома формула закону Ома
U = IR, (8.1)
де U і 
— падіння електричної напруги (різниця електричних потенціалів) на резисторі і сила струму, вимірювані у вольтах (В) і амперах (А) відповідно (рис. 8.1, а); R — опір резистора, вимірюваний в омах (Ом = В/А). Величину g = 1 /R називають провідністю резистора, одиницею виміру якої є сименс (См = 1/Ом).
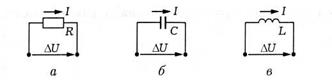
Рис. 8.1
Електрична енергія, що витрачається на подолання опору при протіканні через резистор струму, переходить в теплову енергію, причому вимірювана у ватах (Вт = В • А) потужність тепловиділення на резисторі рівна
W = I 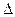U = I 2 R = 
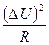= g(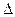 U) 2. (8.2)
Електричний конденсатор володіє властивістю нагромаджувати електричний заряд Qe, вимірюваний в кулонах (Кл), пропорційно різниці потенціалів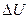 
на його обкладаннях, причому Qe = 
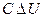, де С — ємність конденсатора, вимірювана у фарадах (Ф). Для конденсатора з постійною ємністю, що ідеалізується, в якому немає перетікання електричного заряду через діелектрик, що розділяє обкладання, при зміні 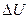в часі t в ланцюзі, що містить послідовно включений конденсатор (рис. 8.1, б), протікає струм силоміць 
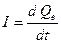, тобто
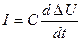, (8.3)
Енергію електричного поля в конденсаторі, рівну Ее = Qe 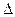U/2 =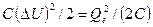 
, вимірюють в джоулях (Дж).
При зміні в часі сили струму, що протікає через індуктивну котушку, виникає електрорушійна сила (ЕРС) самоіндукції, що перешкоджає зміні сили струму (рис. 8.1, в). В разі котушки, що ідеалізується (без опору), цю ЕРС можна представити як різниця потенціалів на кінцях котушки, де L — її індуктивність, вимірювана
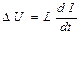(8.4)
в генрі (Гн). При проходженні електричного струму через котушку кожен її виток пронизує деякий магнітний виток. Для котушки індуктивності приймають, що цей потік однаковий для всіх витків (говорять, що він “зчеплений” з кожним витком) і рівний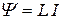 
. Величину називають потокозчепленням і вимірюють у веберах (Вб). Енергія магнітного для котушки, вимірювана в Дж, рівна Ет = 
.
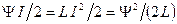Таким чином, ММ резистора є рівняння алгебри, а для конденсатора і індуктивної котушки ММ має форму звичайного диференціального рівняння першого порядку. Якщо вважати, що R, С і L в (8.1) - (8.4) не залежать від сили струму і напруги, то ці рівняння встановлюють лінійний зв'язок між I і U, що є ознакою лінійності ММ.
Разом з пасивними двополюсниками до типових елементів електричних ланцюгів відносять джерела напруги і струму, умовне позначення яких представлене на рис. 8.2, а і б відповідно. Ідеальне джерело електричної напруги є двополюсником, що задає на своїх полюсах зміну в часі t по певному закону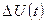 
різниці напруги, не залежною від значення I (t) сили струму, що протікає через нього. Це означає, що таке джерело має настільки малий внутрішній опір 
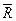, що падінням напруги I (t) на такому опорі можна нехтувати в порівнянні з 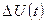. Навпаки, ідеальне джерело електричного струму — це двополюсник, що володіє настільки великим внутрішнім опором 
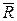, що змінюється за певним
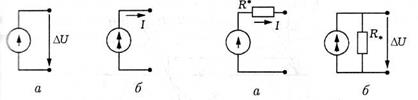
Рис. 8.2 Рис. 8.3
законом I (t) сила струму, що проходить через таке джерело, не залежить від різниці U (t) напруги на його полюсах тобто величиною 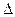U (t) можна нехтувати в порівнянні з 
.
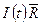Практично джерело струму, близьке до ідеального, можна отримати послідовним з'єднанням джерела досить великої напруги і резистора з опором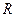 
*, що істотно перевершує опір зовнішньому електричного ланцюгу (рис. 8.3, а). Близьким до ідеального джерела напруги буде двополюсник, що складається з паралельно сполучених джерела струму і резистора з опором 
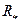, суттєво меншим опору зовнішнього ланцюгу (рис. 8.3, б).
Нехай через резистор тече змінний за часом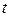 
струм силою
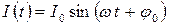, (8.5)
де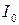 
— амплітуда коливань сили струму, 
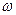— кутова частота і 
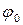— початкова фаза коливань. Величину 
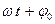називають фазою коливань. Відповідно до закону Ома для падіння напруги на резисторі з опором R отримаємо
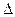UR{t) = I(t)R = 
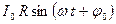, (8.6)
Таким чином, для резистора сила струму і падіння напруги мають однакову початкову фазу коливань (говорять, що вони збігаються по фазі), тобто ці величини одночасно досягають нульових, максимальних і мінімальних значень (рис. 8.4). У цьому
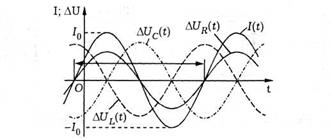
Рис. 8.4
випадку середня за період T =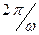 
коливань сили струму потужність тепловиділення на резисторі рівна
,
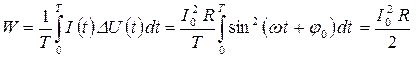тобто вона удвічі менше найбільшого миттєвого значення потужності, відповідного проходженню через той же резистор постійного струму силоміць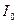 
.
Якщо струм, що змінюється згідно з законом (8.5), тече через котушку з індуктивністю L, то відповідно до (8.4) на котушці виникне падіння напруги
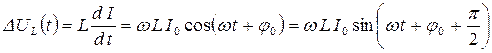. (8.7)
Враховуючи (8.3), нескладно встановити, що для протікання такого струму в ланцюзі, зовнішньому по відношенню до конденсатора ємністю С, падіння напруги на конденсаторі повинне змінюватися згідно із законом
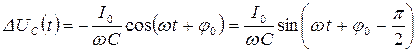. (8.8)
Отже, для конденсатора зміна падіння напруги відстає по фазі на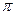 
/2 від зміни сили струму, а для індуктивної котушки, навпаки, випереджає на 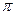/2 (див. рис. 8.4).
Використовуючи показову форму представлення комплексного числа і формулу Ейлера [1], замість (8.5) -(8.8) запишемо комплексні представлення відповідних функцій:
, 
,
, 
,
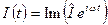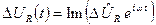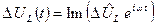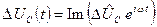де -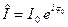 
, 
, 
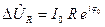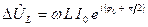і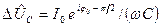 
—
комплексні амплітуди сили струму і відповідних падінь напруги,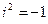 
, 
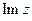— уявна частина комплексного числа 
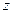. Відношення
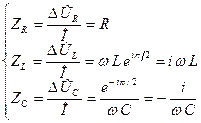, (8.9)
називають комплексними опорами відповідних електричних двополюсників або імпедансами (від латинського слова impedio —
— перешкоджаю). При струмі, що змінюється за законом (8.5) говорять про активний опір резистора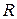 
, індуктивний опір L котушки і ємкісний опор 1/( 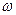C) конденсатору. Останні два терміни об'єднують загальним терміном «реактивний опір».
Якщо резистор, індуктивну котушку і конденсатор розглядати як ланка, що перетворює вхідний сигнал (силу струму I (t)) у вихідний сигнал (падіння напруги), то відповідний комплексний опір називають комплексним передавальним числом такої ланки або комплексним коефіцієнтом підсилення. Залежності модуля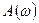 
комплексного передавального числа і головного значення аргументу 
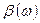цього числа від кутової частоти 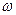називають відповідно амплітудно-частотною і фазово-частотною характеристиками ланки. За допомогою цих характеристик комплексне передавальне число Z можна представити у вигляді Z = 
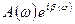. На рис. 8.5 відповідними індексами відмічені ці характеристики для резистора, індуктивною котушки і конденсатора.
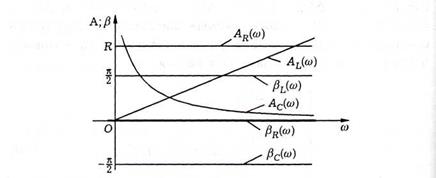
Рис. 8.5
Зауваження 8.1. Підкреслимо ще раз, що розглянуті двополюсники ідеалізуються, оскільки при побудові їх ММ використані спрощені розрахункові схеми реальних елементів електричних ланцюгів (див. [1]). До відмічених вище допущень слід додати, що не врахована кінцева швидкість поширення електричних і магнітних полів, тобто ці ММ є квазістаціонарними математичними моделями. Таке допущення не наводить до помітних похибок, якщо найменша тривалість процесів, що протікають в цих двополюсниках, задовольняє умові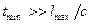 
, 
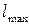— найбільший лінійний розмір електричного ланцюга, 
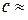2, 9979 • 108 м/с — швидкість світла у вакуумі. При виконанні цієї умови можна нехтувати впливом на характеристики двополюсників хвилевих процесів в електричних елементах і сполучних дротах.
У лінійній ММ процесу, що описується періодичною функцією часу, можна розглядати окремо вплив кожної гармоніки в розкладі цієї функції в ряд Фур'є, а в разі неперіодичного процесу — вплив функції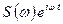 
, де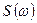 
— відповідна спектральна функція [1]. Але використання гармонік і спектральних функцій при великих значеннях може привести до значних погрішностей квазістаціонарних ММ, оскільки при цьому зменшується значення 
.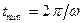