Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обчислення при використанні критерію Колмогорова — Смірнова
|
|
| Число запитів | I Частота, що спостері- гається | II Ймовірність що спостеріг. | III Теоретична ймовірність | IV Інтегральнаймовірність II | V Інтегральнаймовірність III | VI Абсолютна різниця (IV-V) |
| 0, 619 | 0, 571 | 0, 619 | 0, 571 | 0, 048 | ||
| 0, 279 | 0, 319 | 0, 898 | 0, 890 | 0, 008 | ||
| 0, 078 | 0, 089 | 0, 976 | 0, 979 | 0, 003 | ||
| 0, 018 | 0, 017 | 0, 994 | 0, 996 | 0, 002 | ||
| 0, 004 | 0, 003 | 0, 998 | 0, 999 | 0, 001 | ||
| 0, 002 | 0, 001 | 1, 000 | 1, 000 | 0, 000 |
У таблиці 7.7 найбільша абсолютна різниця 0, 048 виходить в групі, відповідній нульовому числу запитів. Саме цю різницю треба порівняти з критичним значенням, знайденим по додатку В.7 [4]. З цієї таблиці видно, що при n = 509 і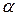 
= 0, 05 критичне значення
.
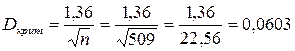Оскільки одержана найбільша різниця 0, 048 менше за критичного значення, не відмовляємося від гіпотези про те, що експериментальний розподіл - пуассонівський.
Природно, виникає питання, коли слід користуватися критерієм 
, а коли критерієм Колмогорова — Смирнова? При відносно малих об'ємах вибірок критерій взагалі непридатний, і слід користуватися критерієм Колмогорова—Смірнова. До того ж, коли об'єм вибірки настільки малий, що для користування критерієм доводиться об'єднувати сусідні групи, потужність цього критерію значною мірою знижується. Однак, якщо об'єм вибірки великий, переважний, по всій ймовірності, критерій .
Кожен з критеріїв має свої сильні і слабкі сторони, і відносно вибору між ними можна дати лише самі загальні вказівки. Критерій дуже потужний для великих вибірок (n > 100); що ж до критерію Колмогорова — Смирнова, то, хоча деякі автори (наприклад, [2, 3]) вказують, що отримували з ним добрі результати лише для n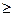 
30, немає достатніх підстав проти вживання цього критерію і при 
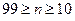. При об'ємі вибірки менше 10 кращих результатів дає, мабуть, критерій Крамера — фон Мізеса [1, 3]. При використанні як критерію, так і критерію Колмогорова — Смирнова дослідник має можливість задати число груп або інтервалів вибірки. Правильний вибір цього числа має велике значення, оскільки воно визначає число ступнів свободи при користуванні критерієм, а взагалі кажучи, чим більше це число, тим надійніше критерій розрізняє характер розподілу. В разі критерію число груп часто визначається з умови, аби в кожну групу попало не менше п'яти експериментальних точок. В той же час в разі використання критерію Колмогорова — Смірнова дані можна як групувати, так і відносити кожне спостереження до окремої групи; остання умова відкриває можливість ефективного аналізу при малих вибірках.
Контрольні запитання
1. Як здійснюється перевірка розподілу одержаних експериментальних даних відповідному певному теоретичному закону розподілу?
2. Перелічити основні теоретичні закони розподілу ймовірностей випадкових величин.
3. Яка характерна властивість середнього і дисперсії пуассонівського закону розподілу ймовірностей?
4. Записати аналітичний вираз для пуассонівського закону розподілу ймовірностей.
5. Навести основне співвідношення для оцінки статистики за критерієм .
6. Що слід враховувати при застосуванні методу перевірки гіпотез за критерієм ?
7. Пояснити основну ідею застосування критерію Колмогорова – Смірнова для перевірки статистичних гіпотез.
8. Перелічити основні умови практичного застосування критеріїв і Колмогорова – Смірнова.