
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дуальні електричні ланцюги
|
|
Побудова математичних моделей технічних систем із типових елементів
Математичні моделі об’єктів, що побудовано із типових елементів. Дуальні електричні ланцюги. Метод електромеханічних аналогій. Використання методу електромеханічних аналогій для моделювання фізичних процесів, що супроводжують роботу технічних систем
Математичні моделі об’єктів, що побудовано із типових елементів
При математичному моделюванні технічного пристрою, в якому протікають процеси різної фізичної природи, перш за все необхідно для кожного з таких процесів виділити типові елементи (див. лекцію 8), створюючи однорідну по фізичних властивостях систему: електричну, механічну, теплову, гідравлічну і тому подібне. Взаємодія елементів в кожній з систем має бути відбита в її розрахунковій схемі (РС). При переході від РС складної системи, що складається з великого числа взаємозв'язаних між собою типових елементів, до її математичної моделі (ММ) макрорівня зручно оперувати еквівалентними схемами, заснованими на аналогіях між ММ елементів, що належать різним фізичним системам. При цьому переважно виявити аналогії між електричною системою і іншими фізичними системами. Ці аналогії дозволяють при побудові ММ таких систем застосовувати досить універсальні прийоми побудови ММ електричних систем, формалізовані з використанням законів Кирхгофа і орієнтованих графів.
Дуальні електричні ланцюги
Під еквівалентною схемою системи, що складається з типових елементів, розуміють їх умовне зображення у вигляді двополюсників і зв'язків між цими двополюсниками. Так математичні моделі (ММ) макрорівня типових елементів різних фізичних систем збігаються формою з ММ електричних двополюсників, то при побудові еквівалентних схем зазвичай використовують позначення, характерні для електричних систем. Еквівалентну схему у вигляді електричного ланцюга, об'єднуючого двополюсники, можна вважати наочною виставою структурною математичною моделі даної системи.
При побудові ММ електричної системи об'єднують ММ вхідних в цю систему типових елементів: резисторів, конденсаторів і індуктивних котушок. Таке об'єднання проводять, застосовуючи до еквівалентної схеми закони Кирхгофа. Перший з них встановлює рівність нулю алгебраїчної суми миттєвих значень сили струму у всіх гілках електричного ланцюга, що мають спільний вузол, а другий — рівність нулю алгебраїчної суми миттєвих значень падінь напруги при обході будь-якого контуру електричного ланцюга в будь-якому напрямі.
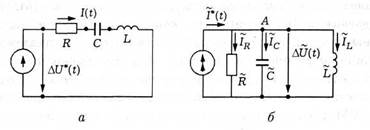
Рис. 9.1
Використання законів Кирхгофа розглянемо на простому прикладі електричного ланцюга, що включає джерело, що задає змінну (у загальному випадку) в часі t напругу 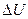 *, резистор опором
*, резистор опором 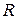 , конденсатор ємністю С і котушку індуктивністю L (рис. 9.1, а). Цей ланцюг складається з одного замкнутого контуру і чотирьох гілок, в кожну з яких включений один з вказаних двополюсників. Застосовуючи до кожного з вузлів цього ланцюга перший закон Кирхгофа, приходимо до висновку, що у будь-який момент часу t сила I електричного струму у всіх гілках однакова. Для падінь електричної напруги на пасивних двополюсниках маємо (див. підрозділ 8.1, лекція 8)
, конденсатор ємністю С і котушку індуктивністю L (рис. 9.1, а). Цей ланцюг складається з одного замкнутого контуру і чотирьох гілок, в кожну з яких включений один з вказаних двополюсників. Застосовуючи до кожного з вузлів цього ланцюга перший закон Кирхгофа, приходимо до висновку, що у будь-який момент часу t сила I електричного струму у всіх гілках однакова. Для падінь електричної напруги на пасивних двополюсниках маємо (див. підрозділ 8.1, лекція 8)
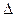 UR = IR,
UR = IR, 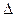 Uc =
Uc = 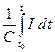 ,
, 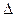 UL =
UL =  , (9.1)
, (9.1)
де to — деякий момент часу, прийнятий за початковий. При обході замкнутого контуру по ходу годинникової стрілки відповідно до другого закону Кирхгофа отримаємо — 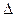 U*(t) +
U*(t) + 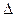 Ur +
Ur + 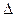 Uc +
Uc + 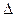 Ul = 0, або з урахуванням (9.1)
Ul = 0, або з урахуванням (9.1)
 . (9.2)
. (9.2)
Як другий приклад розглянемо електричний ланцюг, що включає разом з пасивними двополюсниками джерело, що задає по певному закону 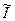 *(t) силу струму (рис. 9.1, б). З другого закону Кирхгофа виходить, що падіння напруги U в кожній з гілок цього ланцюга в будь-який фіксований момент часу t однаково. Для струмів в гілках, що містять пасивні двополюсники, запишемо (див. підрозділ 8.1, лекція 8)
*(t) силу струму (рис. 9.1, б). З другого закону Кирхгофа виходить, що падіння напруги U в кожній з гілок цього ланцюга в будь-який фіксований момент часу t однаково. Для струмів в гілках, що містять пасивні двополюсники, запишемо (див. підрозділ 8.1, лекція 8)
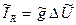 ,
, 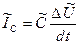 ,
,  , (9.3)
, (9.3)
де  — провідність резистора опором
— провідність резистора опором 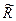 . Всі гілки цього ланцюга сходяться в два вузли. Застосовуючи перший закон Кирхгофа до одного з вузлів (наприклад, до вузла А), отримаємо
. Всі гілки цього ланцюга сходяться в два вузли. Застосовуючи перший закон Кирхгофа до одного з вузлів (наприклад, до вузла А), отримаємо 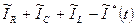 =0, або, враховуючи (9.3)
=0, або, враховуючи (9.3)
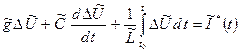 , (9.4)
, (9.4)
Таким чином, ММ розглянутих електричних ланцюгів включають ідентичні формою рівняння (9.2) і (9.4), що містять окрім часу t різні величини. Відповідність між цими величинами представлена в таблиці 9.1.
Таблиця 9.1
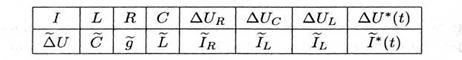
Два електричні ланцюги, ММ яких задовольняють вказаній відповідності величин, прийнято називати дуальними. При цьому залежності (9.1) для падінь напруги на пасивних двополюсниках в одному ланцюзі аналогічні залежностям (9.3) для струмів, що протікають через такі двополюсники в дуальному ланцюзі, і навпаки. Якщо зв'язок між законами зміни напруги і сили струму джерел в дуальних ланцюгах підкоряється залежності 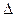 *U(t)=
*U(t)= 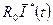 де
де 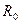 — коефіцієнт пропорційності, що має розмірність опору, то із зіставлення (9.1), (9.2) і (9.3), (9.4) можна встановити, що
— коефіцієнт пропорційності, що має розмірність опору, то із зіставлення (9.1), (9.2) і (9.3), (9.4) можна встановити, що
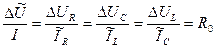 (9.5)
(9.5)
при виконанні умов
 . (9.6)
. (9.6)
Існують правила перетворення складних електричних ланцюгів в дуальних. При цьому число вузлів дуального ланцюга на одиницю перевищує число простих замкнутих контурів вихідного ланцюга (до простих відносять такі замкнуті контури, внутрішня лінія обходу яких не пересікає гілок ланцюга).
Перевіркою правильності перетворення ланцюга в дуальну служить здобуття вихідного ланцюга шляхом побудови дуального ланцюга по відношенню до дуальної. Дуальність електричних ланцюгів дозволяє розширити можливості побудови і перетворення еквівалентних схем стосовно різних фізичних систем (перш за все до механічних систем).
Припустимо, що сила струму в електричному ланцюзі, що представлений на рис. 9.1, а, змінюється за законом I(t) =  ,, де
,, де  - амплітуда коливань сили струму,
- амплітуда коливань сили струму, 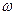 — кутова частота коливань. З'ясуємо, при якому законі
— кутова частота коливань. З'ясуємо, при якому законі 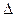 U* (t) зміни напруги джерела це можливо. Для цього заздалегідь продиференціюємо по t (9.2) і запишемо
U* (t) зміни напруги джерела це можливо. Для цього заздалегідь продиференціюємо по t (9.2) і запишемо
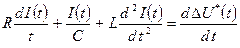
або після підстановки виразу для I (t)
 .
.

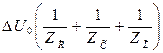 ,
,
причому  ,
,  и
и  . Оскільки комплексна амплітуда падіння напруги
. Оскільки комплексна амплітуда падіння напруги 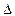 U(t) =
U(t) =  =
=  рівна
рівна  =
= 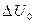 , то
, то
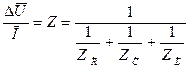 .
.
Отже, при паралельному з'єднанні електричних двополюсників сума їх комплексної провідності, обернених комплексним опорам, дає повну комплексну провідність ланцюга, зворотну її повному комплексному опору.