
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Визначення законів розподілів часових рядів по даних спостережень
|
|
Варіаційний ряд. В результаті проведення спостережень над деякою випадковою величиною 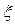 або часовим ергодичним рядом
або часовим ергодичним рядом 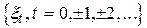 отримуємо ряд чисел
отримуємо ряд чисел
 ,
,
який називається вибіркою. Число 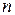 називається обсягом вибірки.
називається обсягом вибірки.
Водночас зауважимо, що часовий ряд являє собою стаціонарний процес з дискретним часом. Він є ергодичним відносно одновимірної функції розподілу  , тому що
, тому що
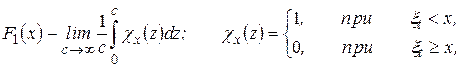 ,
,
тоді і тільки тоді, якщо
 .
.
Стаціонарний ряд з незалежними значеннями - ергодичний відразу, тобто
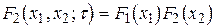 .
.
Якщо всі елементи вибірки розташувати в порядку збільшення їх значень, тобто 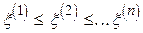 , то отримаємо варіаційний ряд
, то отримаємо варіаційний ряд 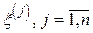 .
.
Кожний елемент варіаційного ряду називається порядковою статистикою. Величина 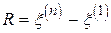 - різниця найбільшого та найменшого значень, називається розмахом варіювання. Деякі порядкові статистики можуть служити статистичними оцінками параметрів, що характеризують випадкову величину
- різниця найбільшого та найменшого значень, називається розмахом варіювання. Деякі порядкові статистики можуть служити статистичними оцінками параметрів, що характеризують випадкову величину 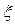 . Наприклад, якщо
. Наприклад, якщо  , то
, то 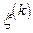 і
і  - називаються вибірковими секстилями і за оцінку средньоквадратичного відхилення
- називаються вибірковими секстилями і за оцінку средньоквадратичного відхилення  випадкової величини
випадкової величини 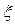 можна взяти вираз
можна взяти вираз
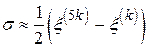 .
.
За оцінку її математичного сподівання 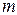 (при непарному
(при непарному 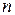 ) беруть
) беруть 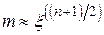 .
.
Частотою деякої події називається відношення кількості наслідків  , що сприяють цій події, до загального числа наслідків
, що сприяють цій події, до загального числа наслідків 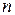 . Позначимо її через
. Позначимо її через 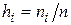 .
.
Вибіркова функція розподілу. В попередньому підрозділі були наведені вирази для обчислення вибіркових моментів. Вони будуть істотно використані далі.
ОЗНАЧЕННЯ 5.4. Вибірковою функцією розподілу для вибірки  обсягом
обсягом 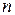 називається функція
називається функція
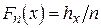 ,
,
де 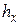 - кількість тих порядкових статистик, значення яких менші
- кількість тих порядкових статистик, значення яких менші  .
.
На рис. 5.4 наведено типовий графік вибіркової (емпіричної) функції розподілу.
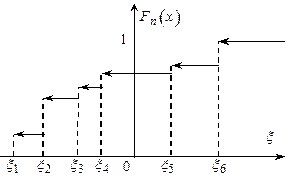
Рис. 5.4
Побудова оцінки щільності розподілу. Спостерігаються значення випадкової величини 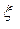 , неперервна щільність розподілу
, неперервна щільність розподілу 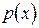 якої невідома і її потрібно оцінити по вибірці з
якої невідома і її потрібно оцінити по вибірці з 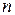 незалежних спостережень
незалежних спостережень  .
.
Розмах варіювання розіб'ємо на 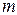 інтервалів довжиною
інтервалів довжиною 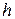 . Емпірична щільність розподілу або “гістограма” вибірки визначається на кожному інтервалі
. Емпірична щільність розподілу або “гістограма” вибірки визначається на кожному інтервалі  довжиною
довжиною 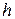 рівністю
рівністю
 ,
,
де  - кількість спостережень, що належать до інтервалу
- кількість спостережень, що належать до інтервалу  . Очевидно, що частота
. Очевидно, що частота 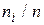 - відображає площу прямокутника, побудованого на
- відображає площу прямокутника, побудованого на  , як на основі з висотою, що дорівнює ординаті гістограми
, як на основі з висотою, що дорівнює ординаті гістограми 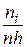 .
.
Таким чином, при великому 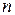 площа прямокутника за теоремою Бернуллі буде наближатися до
площа прямокутника за теоремою Бернуллі буде наближатися до 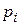 - ймовірності потрапити значенню випадкової величини
- ймовірності потрапити значенню випадкової величини 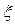 до інтервалу
до інтервалу  :
:
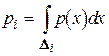 .
.
Тому
 ,
,
де 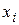 - деяка точка на інтервалі
- деяка точка на інтервалі  .
.
Дисперсія
D 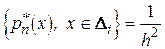 D
D 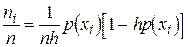 ,
,
тобто при 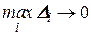 та
та 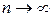 гістограма буде незсуненою і слушною оцінкою для щільності розподілу. Крім того, із ймовірністю, близькою до 1, при великому
гістограма буде незсуненою і слушною оцінкою для щільності розподілу. Крім того, із ймовірністю, близькою до 1, при великому 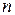 гарантується рівномірне наближення
гарантується рівномірне наближення 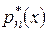 до
до 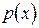 .
.
Гістограма. Якщо спостережень дуже багато, 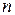 - велике, то незручно будувати графік вибіркової функції розподілу
- велике, то незручно будувати графік вибіркової функції розподілу 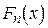 . В цьому випадку користуються групуванням результатів спостережень. А саме, весь інтервал спостережень ділять на
. В цьому випадку користуються групуванням результатів спостережень. А саме, весь інтервал спостережень ділять на 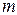 підінтервалів і будують таблицю
підінтервалів і будують таблицю
| Інтервали | 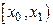
| 
| ... | 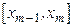
|
Частоти 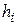
| 
| 
| ... | 
|
де 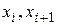 - границі інтервалів,
- границі інтервалів, 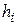 - частота, що відповідає
- частота, що відповідає  - му інтервалу,
- му інтервалу, 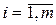 , тобто кількість значень
, тобто кількість значень  , що потрапили в
, що потрапили в  - тий інтервал, віднесене до
- тий інтервал, віднесене до 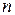 . Переважно
. Переважно 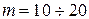 . Довжини інтервалів не обов'язково однакові.
. Довжини інтервалів не обов'язково однакові.
Наведена вище таблиця, оформлена у вигляді графіка називається гістограмою. Інакше кажучи, гістограма - це вибіркова щільність розподілу. Будується вона так. По осі абсцис відкладаються інтервали і на кожному з них, як на основі, будується прямокутник, площа якого дорівнює частоті цього інтервалу. Приклад гістограми наведений на рис. 5.5.
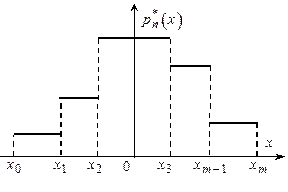
Рис. 5.5
Згладжування гістограм. Задача згладжування гістограм не має однозначного розв'язку, а тому результати її рішення істотно залежать як від використовуваної методики, так і від додаткових вимог, що використовуються в ході її рішення.
Класичним прикладом розв’язування задачі згладжування є згладжування по кривих К.Пірсона. При цьому використовується метод моментів, згідно якого спочатку обчислюються величини
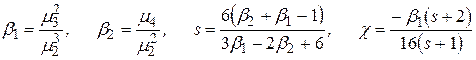 .
.
Потім в залежності від значення параметра 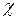 (“капа Пірсона”) вибирається тип основної згладжуючої кривої, а саме:
(“капа Пірсона”) вибирається тип основної згладжуючої кривої, а саме:
1-й тип при 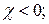 4-й тип при
4-й тип при 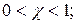 6-й тип при
6-й тип при 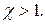
Значення інших параметрів 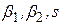 дають можливість вибирати проміжний тип кривої - згладжуючої гістограму згідно методики К.Пірсона [2, …, 4]. Якість згладжування можна оцінити з допомогою статистичних критеріїв. Найбільш вживаний в цьому випадку
дають можливість вибирати проміжний тип кривої - згладжуючої гістограму згідно методики К.Пірсона [2, …, 4]. Якість згладжування можна оцінити з допомогою статистичних критеріїв. Найбільш вживаний в цьому випадку 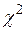 - критерій, запропонований К.Пірсоном.
- критерій, запропонований К.Пірсоном.
Контрольні запитання
1. Пояснити зв’язок між емпіричними моментами і моментами випадкової величини.
2. Навести формули для обчислення емпіричних початкових і центральних моментів.
3. Як визначити емпіричний коефіцієнт асиметрії? На прикладі гауссового розподілу показати, в яких випадках 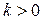 і в яких
і в яких 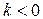 .
.
4. Як визначити емпіричний коефіцієнт ексцесу? На прикладі гауссового розподілу показати, в яких випадках 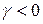 і в яких
і в яких  .
.
5. Як обчислюється лінійний зв’язок між двома випадковими величинами:
a. а) в ймовірнісному (теоретичному) розумінні?
b. б) при обробці даних спостережень?
6. Які властивості має коефіцієнт кореляції двох випадкових величин?
7. Навести властивості емпіричного коефіцієнта кореляції.
8. Для заданої вибірки обсягу 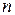 навести методику побудови варіаційного ряду.
навести методику побудови варіаційного ряду.
9. Що означають терміни «статистика», «порядкова статистика»?
10. Для випадкової події дати тлумачення «частота події» і «ймовірність події», зв’язок між ними.
11. Чим відрізняється початковий момент 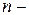 го порядку випадкової величини від початкового вибіркового (емпіричного) моменту?
го порядку випадкової величини від початкового вибіркового (емпіричного) моменту?
12. Навести формули для обчислення центральних вибіркових моментів.
13. Як обчислити вибіркові коефіцієнти асиметрії і ексцесу?
14. Яка методика побудови вибіркової функції розподілу шляхом обробки даних спостережень?
15. Як при побудові емпіричної щільності розподілу або гістограми визначається:
а) число інтервалів розбиття розмаху варіювання варіаційного ряду?
б) ординати гістограми?
в) дисперсія ординат гістограми?
16. Які властивості має гістограма як статистична оцінка щільності розподілу ймовірностей?
17. Дати приклад розв’язування задачі згладжування гістограми.