
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оцінка середнього і кореляційної функції часового ряду
|
|
Оцінка середнього. Нехай 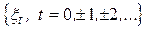 - дійсний гільбертів слабо стаціонарний процес з невідомим математичним сподіванням
- дійсний гільбертів слабо стаціонарний процес з невідомим математичним сподіванням 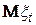 , для якого відносно першого і другого моментів виконується ергодична теорема, тобто
, для якого відносно першого і другого моментів виконується ергодична теорема, тобто
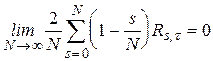 при всіх
при всіх 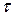 .
.
Зауважимо, що на відміну від попередніх параграфів, тут випадкові величини 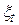 корельовані. В результаті спостереження отримуємо вибірку (реалізацію)
корельовані. В результаті спостереження отримуємо вибірку (реалізацію)
 ,
,
використовуючи яку, будується лінійна оцінка
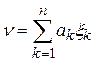 . (5.7)
. (5.7)
Для того, щоб ця оцінка була незсуненою, необхідно, щоб математичне сподівання
 ,
,
тобто дійсні коефіцієнти  , повинні задовольняти умові
, повинні задовольняти умові  . В подальшому будемо припускати
. В подальшому будемо припускати  .
.
Щоб оцінити якість оцінки (5.7), можна скористатися, наприклад, нерівністю Чебишева, але для цього потрібно знати дисперсію оцінки.
Якщо відома кореляційна функція 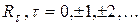 процесу, то дисперсія випадкової величини
процесу, то дисперсія випадкової величини 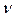 визначається виразом (для випадку незалежних
визначається виразом (для випадку незалежних 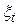 ми це вже підраховували)
ми це вже підраховували)
D 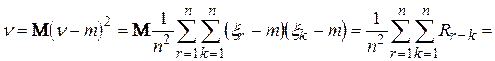
 .
.
D 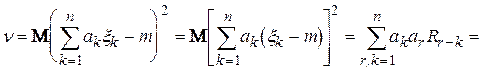
 .
.
На рис. 5.3 ілюструється спосіб підсумовування при переході до одинарної суми в останньому виразі. Значення кореляційної функції 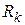 в усіх цілочисельних точках на кожній похилій лінії стале. А їх кількість на 1 зменшується при переході від однієї лінії до іншої. Таким чином, після заміни порядку підсумовування остаточно одержуємо
в усіх цілочисельних точках на кожній похилій лінії стале. А їх кількість на 1 зменшується при переході від однієї лінії до іншої. Таким чином, після заміни порядку підсумовування остаточно одержуємо
D 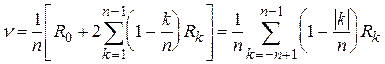 . (5.8)
. (5.8)
Із останнього виразу видно, що із зростанням 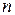 до нескінченності дисперсія D
до нескінченності дисперсія D 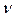 прямує до нуля, тобто оцінка (5.7) є слушною. Використовуючи нерівність Чебишева можна знайти довірчий інтервал для цієї оцінки.
прямує до нуля, тобто оцінка (5.7) є слушною. Використовуючи нерівність Чебишева можна знайти довірчий інтервал для цієї оцінки.
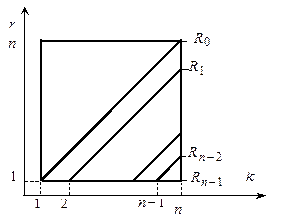
Рис. 5.3
Оцінка кореляційної функції. Припустимо тепер, що процес 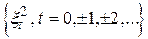 є гільбертовим, тобто
є гільбертовим, тобто  , слабо стаціонарним і задовольняє ергодичній теоремі
, слабо стаціонарним і задовольняє ергодичній теоремі
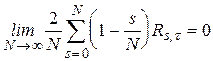 при всіх
при всіх 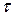 .
.
Це допущення буде виконуватися, якщо вимагати, щоб, чотиривимірна функція розподілу процесу 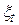 не залежала від початку відліку. Тоді оцінкою кореляційної функції
не залежала від початку відліку. Тоді оцінкою кореляційної функції 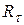 процесу
процесу 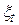 є функція
є функція
 . (5.9)
. (5.9)
Графік функції 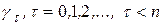 , переважно називають корелограмою. Для оцінки (5.9) існує зсув, який наближено можна визначити з виразу
, переважно називають корелограмою. Для оцінки (5.9) існує зсув, який наближено можна визначити з виразу
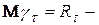 D
D  , (5.10)
, (5.10)
де D 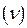 - дисперсія оцінки
- дисперсія оцінки 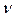 , що визначається згідно (5.8), і
, що визначається згідно (5.8), і 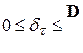
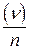 при
при 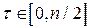 . Однак оцінка (5.9) – асимптотично незсунена. Зсув для оцінки (5.9) є “платою” за незнання точного значення
. Однак оцінка (5.9) – асимптотично незсунена. Зсув для оцінки (5.9) є “платою” за незнання точного значення 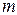 , але якщо в (5.9) випадкову величину
, але якщо в (5.9) випадкову величину 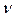 замінити на
замінити на 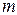 , то отримана таким чином оцінка стає незсуненою, тобто тоді D
, то отримана таким чином оцінка стає незсуненою, тобто тоді D 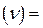 D
D 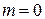 , а значить і
, а значить і 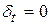 при будь-якому
при будь-якому 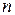 . Щоб оцінити якість оцінки (5.9) аналогічно попередньому випадку, потрібно знати принаймні її дисперсію. В зв’язку з тим, що формула для визначення D
. Щоб оцінити якість оцінки (5.9) аналогічно попередньому випадку, потрібно знати принаймні її дисперсію. В зв’язку з тим, що формула для визначення D 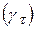 дуже складна, зупинимось на обчисленні дисперсії в припущенні, що в (5.9) замість
дуже складна, зупинимось на обчисленні дисперсії в припущенні, що в (5.9) замість 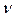 стоїть
стоїть 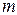 , тобто відомо математичне сподівання процесу
, тобто відомо математичне сподівання процесу 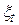 . В цьому випадку замість
. В цьому випадку замість  будемо писати
будемо писати  , де
, де
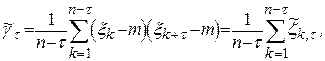
де
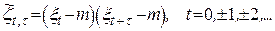 .
.
Обчислення дисперсії оцінки  вимагає розгляду моментів четвертого порядку для процесу
вимагає розгляду моментів четвертого порядку для процесу 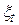 , тому вище і була вимога щодо їх існування.
, тому вище і була вимога щодо їх існування.
Для процесу 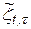 математичне сподівання в будь-який момент часу, тобто незалежно від
математичне сподівання в будь-який момент часу, тобто незалежно від  , дорівнює
, дорівнює
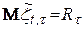 ,
,
а кореляційна функція
 .
.
Відзначимо, що для того, щоб функція 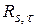 не залежала від початку відліку, недостатньо вимагати лише стаціонарності у широкому розумінні процесу
не залежала від початку відліку, недостатньо вимагати лише стаціонарності у широкому розумінні процесу 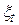 , тобто ця умова не забезпечує незалежності від початку відліку моменту другого порядку процесу
, тобто ця умова не забезпечує незалежності від початку відліку моменту другого порядку процесу 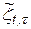 . Останнє забезпечується вимогою незалежності від початку відліку чотиривимірної функції розподілу процесу
. Останнє забезпечується вимогою незалежності від початку відліку чотиривимірної функції розподілу процесу 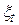 .
.
Таким чином, ми знову приходимо до задачі, яку розв’язували в попередньому пункті, але тепер для процесу 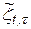 . Тому дисперсія оцінки
. Тому дисперсія оцінки  з врахуванням (5.8) матиме такий вигляд:
з врахуванням (5.8) матиме такий вигляд:
D 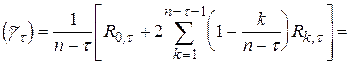
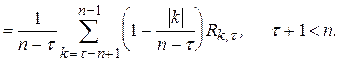 (5.11)
(5.11)
Обчислення D 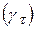 , коли
, коли 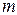 невідомо і замінене на
невідомо і замінене на 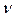 , пов’язане з додатковими труднощами.
, пов’язане з додатковими труднощами.