Емпіричні моменти та їх обчислення

Емпіричні моменти. Емпіричні (вибіркові) моменти за своєю структурою повністю відповідають теоретичним моментам розподілу, що розглядались раніше, і є їх статистичними оцінками.

Обчислюються емпіричні моменти за отриманими результатами спостережень випадкової (вимірюваної) величини 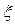, тобто є функціями від випадкових аргументів, тому й самі є випадковими. Припустимо, що у нашому розпорядженні є вибірка 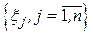обсягу 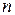, отримана в результаті спостережень над .

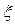Емпіричні початкові моменти визначаються згідно формули

, (5.1)

де 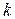- порядок емпіричного моменту (інколи для узагальнення формул робиться припущення ).

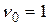Емпіричні центральні моменти визначаються таким чином:

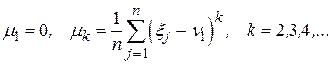, (5.2)

де 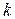- порядок моменту, а 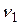- визначається згідно (5.1).

Виходячи з (5.2) й використовуючи формули бінома і (5.1), легко побачити, що емпіричні центральні моменти зв'язані з початковими моментами наступними співвідношеннями:

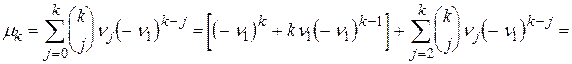
. (5.3)

Зокрема,

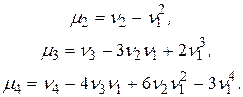
Таким чином, емпіричні моменти зв'язані між собою співвідношеннями, аналогічними до співвідношень між теоретичними моментами.

ОЗНАЧЕННЯ 5.1. Емпіричним коефіціентом асиметрії називається величина, що визначається виразом

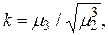(5.4)

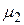де та 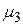визначаються згідно (5.2).

Цей коефіцієнт характеризує асиметрію емпіричної (вибіркової) щільності розподілу відносно емпіричного середнього (рис. 5.1). Якщо 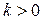, то маємо ’’праву’’ асиметрію, якщо 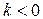то - ’’ліву’’.

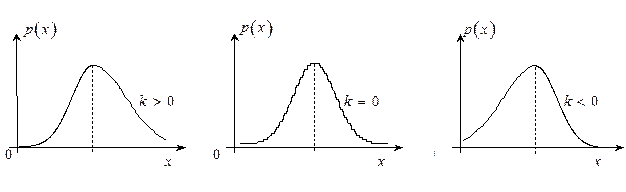Рис. 5.1

ОЗНАЧЕННЯ 5.2. Емпіричним коефіцієнтом ексцесу називається величина

. (5.5)

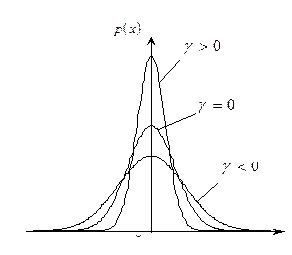
Рис. 5.2

Існує точка зору, що коефіцієнт ексцесу 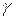характеризує поведінку функції щільності розподілу в околі вершини у порівнянні з кривою гауссового розподілу (рис. 5.2). В загальному випадку це твердження невірне, але є багато розподілів, коли це так, наприклад, для розподілів, які розглядаються нижче, це має місце.

Зауважимо, що формули (5.1), (5.2), (5.4), (5.5) є прикладами точкових оцінок, розглянутих в попередніх лекціях.

Емпіричний коефіцієнт кореляції. Як відзначалося в попередніх підрозділах та у відомих роботах (див., наприклад. [2, 4]), теоретичний коефіцієнт кореляції двох гільбертових випадкових величин 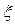і визначається по формулі

,

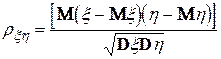і характеризує міру сили (тісноти) та напрямку лінійного зв'язку між 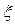і .

Зупинимося тепер на питанні, яким чином по отриманій внаслідок спостережень над величинами 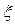і вибірці і представленій множиною пар чисел , де 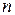- обсягу вибірки, побудувати емпіричний коефіцієнт кореляції.

ОЗНАЧЕННЯ 5.3. Емпіричним коефіцієнтом кореляції називають залежну від результатів спостережень величину

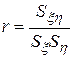, (5.6)

де

,

,

, .

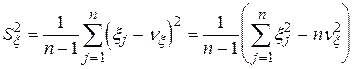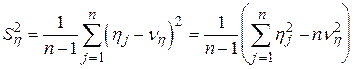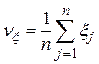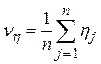Зауважимо, що, як і теоретичний коефіцієнт кореляції 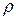, емпіричний коефіцієнт кореляції 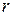задовольняє умові .

Якщо 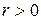, то більшим значенням відповідають загалом більші значення 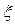, а при 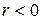- навпаки. Тому в цих випадках говорять про додатну або від'ємну кореляцію.