Математичне сподівання и дисперсію.

Будьякий випадковий процес зручно розглядати у вигляді суми статичної, тобто незалежної від часу складової і динамічної, або флуктуаційної складової.

Статичну складову можна одержати, обчислюючи середнє значення (математичне сподівання), яке являє собою просто середнє з усіх значень досліджуваного випадкового процесу 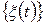. Аналітично це середнє значення визначається наступним співвідношенням

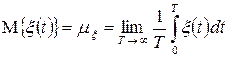, (3.6)

де М – оператор математичного сподівання.

Динамічна складова визначається дисперсією випадкового процесу 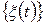, а саме

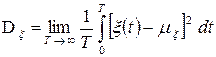. (3.7)

Позитивне значення кореня квадратного з дисперсії носить назву середньоквадратичного відхилення

.

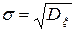Параметри, що визначаються співвідношеннями (3.6) та (3.7) носять назву числових характеристик випадкових процесів.