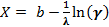Алгоритмические ГСЧ

1) Метод серединных квадратов

Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее из R1 берется середина (четыре средних цифры) — новое случайное число — и записывается в R0. Затем процедура повторяется

Недостатки метода: 1) если на некоторой итерации число R0 станет равным нулю, то генератор вырождается, поэтому важен правильный выбор начального значения R0; 2) генератор будет повторять последовательность через Mn шагов (в лучшем случае), где n — разрядность числа R0, M — основание системы счисления.

2) Метод серединных произведений

Число R0 умножается на R1, из полученного результата R2 извлекается середина R2* (это очередное случайное число) и умножается на R1. По этой схеме вычисляются все последующие случайные числа

3) Линейный конгруэнтный метод

Линейный конгруэнтный метод является одной из простейших и наиболее употребительных в настоящее время процедур, имитирующих случайные числа. В этом методе используется операция mod(x, y), возвращающая остаток от деления первого аргумента на второй. Каждое последующее случайное число рассчитывается на основе предыдущего случайного числа по следующей формуле: 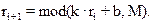M — модуль (0 < M); k — множитель (0 ≤ k < M); b — приращение (0 ≤ b < M); r0 — начальное значение (0 ≤ r0 < M). Последовательность случайных чисел, полученных с помощью данной формулы, называется линейной конгруэнтной последовательностью.
23. Методы моделирования непрерывных случайных величин. Сущность метода обратной функции.

Непрерывная случайная величина далее – НПВ.

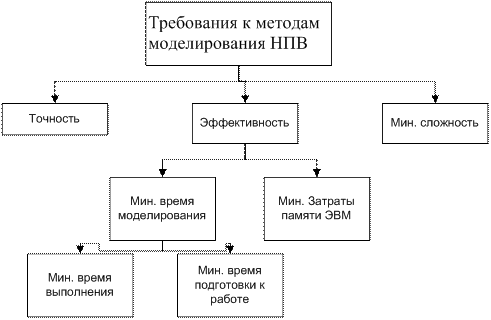
Выделяют следующие методы моделирования НПВ:

· Метод обратной функции;

· Табличный метод;

· Метод композиций;

· Метод кусочно-линейной аппроксимации законов распределения;

· Метод Неймана.

и F(x) = γ

Приравняем левые части обоих выражений.

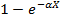= γ Отсюда: 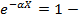γ

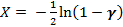Упрощая, получим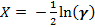

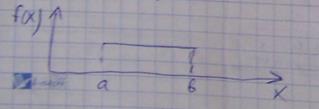
Случайная величина Х распределена по равномерному закону на интервале [a, b]

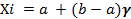
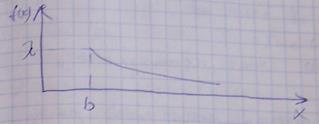
Случайная величина Х распределена по сдвинутому экспоненциальному закону с параметрами λ и b.