Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналитические модели одноканальных СМО с отказами и с ожиданием
|
|
Величины P0, Pотк, q рассчитываются по разному в зависимости от типа СМО.
1) Точный расчет возможен для Марковских СМО на основе аналитических зависимостей.
2) Приближенный расчет возможен для любых типов СМО методами имитационного моделирования.
Одноканальные СМО с отказами
М/М/1/0
Граф состояний
 |
S0 – канал свободен
S1 – канал занят
P0(t) – вероятность состояния «канал свободен»
P1(t) – вероятность состояния «канал занят»
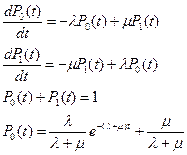
При t стремящимся к бесконечности 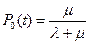
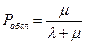
Одноканальная СМО с ожиданием
М/М/1/N-1
 |
S0 – канал свободен
S1 – канал занят, в очереди 1 заявка
Sn – канал занят, в очереди N-1 заявка
15. Аналитические модели многоканальных СМО с отказами и с ожиданием. 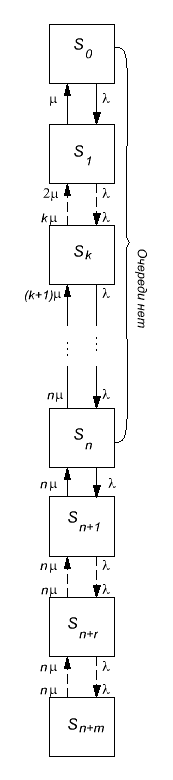
Состояния системы: 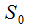 - ни один канал не занят;
- ни один канал не занят; 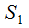 - среди свободных каналов только один является занятым.…
- среди свободных каналов только один является занятым.…  - среди свободных занято
- среди свободных занято 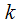 каналов; …
каналов; …  - среди всех
- среди всех 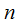 каналов нет ни одного свободного. Рядом со стрелками обозначены интенсивности соответствующих потоков событий. По стрелкам слева направо переходу системы способствует поток заявок, интенсивность которого составляет
каналов нет ни одного свободного. Рядом со стрелками обозначены интенсивности соответствующих потоков событий. По стрелкам слева направо переходу системы способствует поток заявок, интенсивность которого составляет  (количество несвободных
(количество несвободных 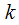 каналов) и поступила очередная заявка, то осуществляется перемещение системы в состояние
каналов) и поступила очередная заявка, то осуществляется перемещение системы в состояние 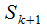 .
.
Найдем интенсивности потоков событий, которые способствуют переходу системы в направлении (стрелки) справа налево. Допустим система находится в состоянии 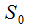 , соответственно, интенсивность потока событий, который заставляет переходить систему из одного состояния в другое по направлению
, соответственно, интенсивность потока событий, который заставляет переходить систему из одного состояния в другое по направлению 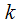 занятых каналах, интенсивность потока составит
занятых каналах, интенсивность потока составит 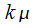 .
.
В соответствии с общими правилами запишем уравнения Колмогорова для вероятностей состояний:
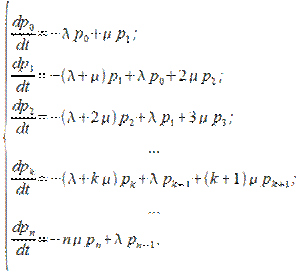 С ожиданием
С ожиданием
Система с ограниченной длиной очереди. Разберем n-канальную СМО с ожиданием, интенсивность приходящих заявок которой равняется 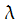 ; интенсивность обслуживания —
; интенсивность обслуживания —  , количество мест в очереди —
, количество мест в очереди —  .
.
Для каждого состояния системы определяется соответствующий числу заявок номер. Эти заявки имеют взаимосвязь с системой.
отсутствие очереди:
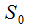 - нет ни одного занятого канала;
- нет ни одного занятого канала; 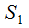 - среди свободных каналов, занятым является только один; …
- среди свободных каналов, занятым является только один; …  - среди свободных заняты только
- среди свободных заняты только 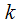 каналы; …
каналы; …  - нет ни одного свободного канала; существует очередь:
- нет ни одного свободного канала; существует очередь: 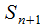 - нет ни одного свободного канала, существует одна очередная заявка;
- нет ни одного свободного канала, существует одна очередная заявка;
… 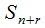 - нет свободных каналов, число очередных заявок —
- нет свободных каналов, число очередных заявок —  ; …
; …  .
.
Отобразим выражения для предельных вероятностей состояний, применяя обозначение 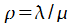 :
:
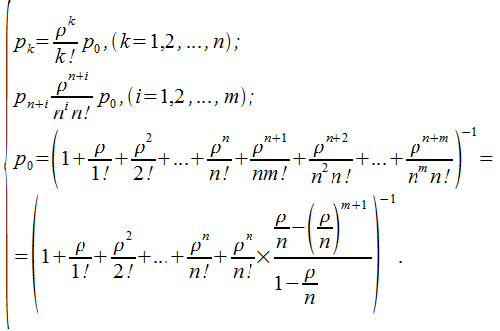 (в данном случае использовано выражение для суммы геометрической прогрессии, знаменатель которой включает
(в данном случае использовано выражение для суммы геометрической прогрессии, знаменатель которой включает 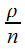 ). Вероятность отказа. Прибывшей в систему заявке может быть отказано в случае, если нет свободных
). Вероятность отказа. Прибывшей в систему заявке может быть отказано в случае, если нет свободных  мест в очереди:
мест в очереди: