Простейший поток заявок и его особенности

Поток заявок называется стационарным, если интенсивность λ и закон распределения A(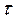) интервалов между последовательными заявками не меняется во времени.

Поток заявок называется ординарным, если в каждый момент времени t_k может появиться только одна заявка.

Поток заявок называется потоком без последствий, если заявки поступают независимо друг от друга.

Стационарный, ординарный поток без последствий называется простейшим.

Интервалы времени 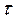между заявками в простейшем потоке распределяются по экспоненциальному закону с функцией распределения A(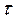)=1- e^-λ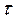

λ > 0 интенсивность распределения, представляет собой интенсивность потока заявок.

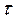≥ 0?

Плотность распределения в соответствии с данным законом записывается в следующем виде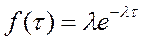

Наиболее вероятной оказываются малые интервалы времени между заявками.

Показано, что экспоненциальный закон распределения в этом смысле является экстремальным, т.е. если система справляется с обслуживанием экспоненциального потока заявок, то она справится и с потоками заявок, распределенных по другим законам.

Мат ожидание в соответствии с данным законом является 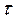, а дисперсия 1/ λ.

Простейший поток заявок часто называют пуассоновским поскольку число заявок k, поступающих за некоторый промежуток времени t, распределено по закону Пуассона.

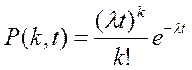где P(k, t) – вероятность поступления k заявок, за некоторый фиксированный интервал времени t.

Особенности простейшего потока заявок:

1. Суммирование потоков

Сумма N независимых стационарных ординарных потоков с интенсивностями 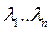образуют простейший поток с интенсивностью 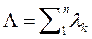при условии, что складывающиеся потоки оказывают более или менее одинаково малое влияние на суммарный поток.

На практике поток близок к простейшему при N≥ 5. При Суммировании независимых простейших потоков суммарный поток будет простейшим при любых условиях.

2.Вероятностное разряжение потоков

Если любую заявку случайным образом с некоторой вероятностью p исключить из потока независимо от того, исключены или нет другие заявки, то образуется простейший поток с интенсивностью 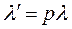где λ – интенсивность исходного потока

Поток исключенных заявок также простейший с интенсивностью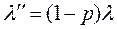

3.Простота. Предположение о простейшем потоке заявок позволяет для многих математических моделей сравнительно легко получать в явном виде зависимости характеристик от параметров.