Модель міжгалузевого балансу Леонтьєва. Коефіцієнти прямих витрат. Матрична форма балансових рівнянь.

У системі балансових рівнянь (2.1) невідомі не тільки обсяги виробництва галузей , які треба знайти, а й обсяги споживання продукцій у сфері виробництва . Тому в розглядуваній системі рівнянь, невідомих більше ніж кількість рівнянь, і вона має невимірну множину розв'язків.

Вихід із цієї ситуації запропонував американський економіст В. В. Леонтьєв (1930 р.). На підставі вивчення структури економіки США у вигляді моделі міжгалузевого балансу.

Балансова модель Леонтьєва базується на таких припущеннях:

1) розглядувані галузі вважаються «чистими», тобто продукція кожної галузі є однорідною (галузь випускає продукцію одного типу і різні галузі випускають різну продукцію);

2) розглядається статична технологія виробництва, яка не змінюється за певний період часу;

3) має місце прямо пропорційна залежність між потоками продукції з одної галузі в другу та об'ємами продукції :

, (2.2)

де - коефіцієнти прямих витрат ().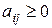

Залежність (2.2) випливає з пропозиції В. В. Леонтьєва про те, що структура витрат у кожної галузі незмінна, тобто коефіцієнти , які характеризують структуру витрат, постійні, тобто

.

Коефіцієнти прямих витрат, як безрозмірні величини, мають подвійне економічне тлумачення:

1) Якщо балансова модель розробляється у натуральних вимірах, величини характеризують кількість одиниць продукції 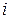-ої галузі, необхідних для виготовлення одиниці 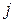-го продукту.

2) Якщо міжгалузевий баланс записується у вартісних вимірах, то є часткою вартості продукції 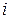-ої галузі у вартості одиниці продукції 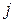-ої галузі.

Підставивши залежності (2.2) у систему рівнянь (2.1), отримаємо систему рівнянь з однією групою невідомих – 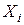, яка може бути легко розв'язана.

Остаточно система рівнянь міжгалузевого балансу або економіко-математична модель міжгалузевого балансу Леонтьєва матиме вигляд

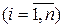, (2.3)

Ця система рівнянь порядку розв'язується відносно невідомих .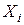

Системі рівнянь (2.3) можна поставити у відповідність систему, записану у матричному виді 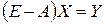, або

, (2.4)

де ‑ ряд змінних ;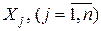

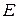‑ одинична матриця порядку ;

‑ матр коефіцієнтів прямих витрат;

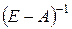‑ обернена матриця Леонетьєва (матриця повних витрат);

‑ праві частини рівнянь .

Приклад 1. Припустимо, що економіка регіону умовно поділена на 4 галузі: промисловість (засоби виробництва) – А; промисловість (предмети споживання) - B; сільське господарство – C; інші галузі – D.

Міжгалузевий баланс цих галузей із зазначенням коефіцієнтів прямих матеріальних витрат і кінцевої продукції, наведений у вигляді умовних витрат, подано у табл. 2.1

Таблиця 2.1

Галузі, що виробляють	Валова продукція	Галузі, що споживають	Продукція у сфері споживання
А	В	С	D
А		0, 2	0, 1	0, 06	0, 2
В		0, 05	0, 2	0, 04	0, 15
С		0, 1	0, 05	0, 04	0, 1	67, 5
D		0, 2	0, 1	0, 1	0, 05

За наведеними даними необхідно знайти обсяги планового випуску валової продукції кожної галузі .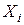

Розв’язання. Складаємо систему рівнянь міжгалузевого балансу (2.3) з використанням поданих у таблиці коефіцієнтів прямих витрат та значень продукції у сфері споживання :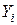

Після спрощення отримаємо систему:

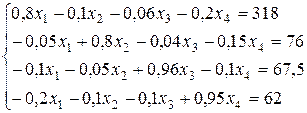(2.5)

Розв’язки цієї системи

Економічне тлумачення отриманих результатів. Для отримання заданих значень кінцевої продукції 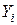в умовних одиницях чотирьох галузей та задоволення виробничо-експлуатаційних потреб цих галузей валова продукція галузі А має становити 480 од., галузі В – 170 од., галузі С – 150 од. та галузі D – 200 од.

Приклад 2. Використавши дані, отимані в прикладі 1, розрахувати міжгалузеві постачання засобів виробництва та скласти міжгалузевий баланс для чотирьох галузей (A, B, C, D).

Розв’язання. Міжгалузеві потоки з однієї галузі в іншу розраховуються за формулою (2.2)

Помноживши подані у табл. 2.1 коефіцієнти прямих витрат на отримані значення валової продукції за галузями 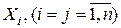, знайдемо розподіл продукції кожної галузі.

Наприклад, розрахуємо розподіл продукції галузі А.

Для власних потреб: 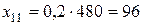од.

Для потреб галузі В: 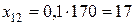од.

Для потреб галузі С: од.

Для потреб галузі D: 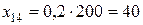од.

Аналогічно розрахуємо розподіл продукції решти галузей і представимо ці результати у вигляді табл. 2.2.

Таблиця 2.2

Галузі, що виробляють	Галузі, що споживають	Плановий обсяг споживання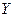
А	В	С	D
А
В
С		8, 5			67, 5
D
Валова продукція
Чиста продукція		93, 5			523, 5

Показники чистої продукції знайдені як різниця валової продукції галузі та суми її виробничих витрат за своєю продукцією і продукції інших галузей. Так чиста продукція галузі А: 480-(96+24+48+96)=216 од.