Коефіцієнти повних витрат

Обернену матрицю Леонтьєва 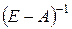позначимо через 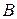, а її елементи ‑ через . Тоді система рівнянь міжгалузевого балансу матиме вигляд

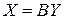, (2.6)

де .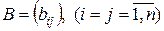

Система рівнянь 2.6 виражає обсяг валової продукції галузей, що виробляють, через обсяги кінцевої продукції таких галузей 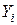, які надходять у сферу споживання.

Коефіцієнти матриці 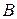називають коефіцієнтами повних витрат. Їх економічне тлумачення полягає в тому, що вони показують, скільки потрібно випустити продукції в 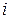- й галузі, щоб була випущена одиниця кінцевої продукції 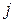-ої галузі.

Матриця 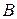у рівнянні (2.6) називається матрицею повних витрат.

Повні витрати становлять суму прямих та побічних (непрямих) витрат продукції галузі 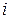на одиницю продукції галузі 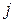. Прямі витрати виражають кількість засобів виробництва, витрачених безпосередньо на виготовлення цього продукту галузі. Непрямі витрати стосуються попередніх стадій виробництва та входять до продукту не прямо, а через інші засоби виробництва.

Приклад 3. Розрахувати показникиповних витрат за даними міжгалузевого балансу прикладу 1.

Розв’язання. Коефіцієнти повних витрат відображають кількість продукції 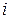- ої галузі, неохідної для випуску одиниці кінцевої продукції 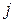-ої галузі. Тому, якщо в системі рівнянь міжгалузевого балансу покласти та розв’язати систему рівнянь відносно , то отримаємо коефіцієнти повних витрат 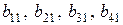, які характеризують матеріальні витрати кожної галузі на випуск одиниці кінцевої продукції першої галузі. Так само розраховують іншіі коефіцієнти повних вират: необхідно в ситсемі (2.3) покласти , а інші значення кінцевого продукту такими, що дорівнюють нулю. Потім покладаємо , а усі решта – нулі, далі так само для .

Відповідно до викладеного, для розрахунку коефіцієнтів повних витрат 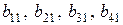у системі (2.5) замість обсягів продукції 318; 76; 67, 5; 62 необхідно поставити відповідно 1, 0, 0, 0, а замість ‑ вказані коефіцієнти повних витрат:

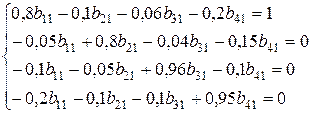
Розв’язавши отриману систему, отримаємо коефіцієнти повних витрат усіх галузей на виробництво одиниці кінцевої продукції галузі А:

.

Аналогічно, розв'язавши ще три системи рівнянь знайдемо коефіцієнти повних витрат кожної галузі на виробництво одиниці кінцевої продукції галузей B, C і D. Отже, отримаємо матрицю повних витрат: