Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение зависимости между показателями
|
|
Пусть рассматриваются два экономических показателя X и Y. Целью является исследование зависимости между ними.
Необходимо выяснить, существует эта зависимость или нет. Если она существует, описать ее формулами, чтобы, зная значение одной, можно было вычислить, какое значение примет другая.
Для этого проводится серия наблюдений, в каждом из которых фиксируются значения обоих величин X и Y. Результатом таких наблюдений является выборка: (x1; y1 )
(x2; y2 )
(x3; y3 )
(x4; y4 )
..........
(xn; yn)
Всего проведено n наблюдений (объем выборки равен n).
 |
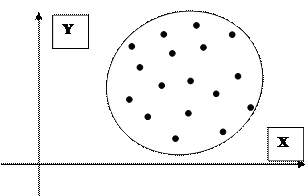
Если данные наблюдений нанести на координатную плоскость, получим корреляционное поле:
При исследовании двух факторов этот построенный график уже показывает, существует зависимость или нет, характер этой зависимости. В частности, на приведенном графике уже видно, что с ростом фактора Х значение результата У тоже увеличивается. Правда зависимость эта нечеткая, размытая, или, правильно говоря, статистическая.
Выделяют следующие типы зависимостей между показателями:
Функциональная зависимость: каждому значению фактора Х соответствует только одно значение результативного признака У.
На корреляционном поле в этом случае мы увидим, что данные наблюдений выстраиваются точно на некоторую линию или кривую.

Статистическая зависимость: при одном и том значении фактора Х результативный признак У может принимать различные значения.
На корреляционном поле в этом случае мы увидим, что данные наблюдений размыты, имеется более или менее значительный разброс данных.
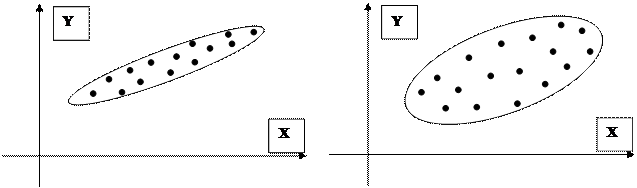 |
В этом случае принято говорить о тесноте статистической зависимости. На левом рисунке представлена тесная статистическая зависимость, на правом – слабая.
Отсутствие зависимости: