Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 2. Метод наименьших квадратов
|
|
2.1. Процедура метода наименьших квадратов
2.2. Предпосылки метода наименьших квадратов
2.1. Процедура метода наименьших квадратов
В записанное уравнение обязательно входят коэффициенты (параметры), и эти коэффициенты нужно находить, определять. Причем сделать это таким образом, чтобы построенное уравнение наилучшим образом описывало данные наблюдений, чтобы линия регрессии проходила как можно ближе к точкам корреляционного поля. Этот этап называется: статистическая оценка параметров регрессии.
Например, изобразим случай, когда корреляционное поле показывает, что можно применить линейную регрессию.
 |
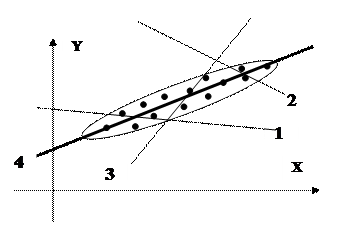В уравнение прямой (y = a x + b) входят два параметра: a и b. Меняя их, получаем различные прямые линии. Выбрать нужно только одну, с конкретными значениями параметров. Ту, которая на рисунке изображена под номером 4.
В общем случае задача ставится таким образом.
Выбрана формула для уравнения регрессии в виде прямой линии:
y = f (x, a, b) или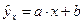 
.
Подобрать параметры регрессии таким образом, чтобы отклонения данных наблюдений от линии регрессии были бы минимальными.
Для решения этой задачи имеется несколько методов. Самый популярный и наиболее часто используемый из них – метод наименьших квадратов (МНК).
Чтобы измерить степень отклонения кривой от экспериментальных точек (или наоборот, экспериментальных точек от кривой, которую мы строим) введем следующее определение:
Отклонением (или остатком, обозначается в литературе по-разному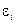 
, 
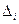либо ui) назовем разность между теоретическим значением 
, подсчитанным по предполагаемой формуле и экспериментальным значением 
:
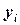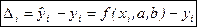
Здесь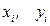 
– это данные наблюдений, известные числа. Покажем эти отклонения на графике:
 |
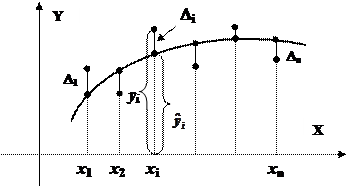Все они должны быть как можно меньше. Этого можно добиться, если взять сумму квадратов этих чисел и потребовать, чтобы она была минимальна:
Σ Δ 2i → min
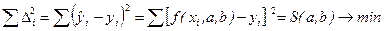
Т.е., эта сумма квадратов является функцией от коэффициентов регрессии, и нужно найти минимум функции нескольких переменных. Из курса высшей математики известно, что для этого нужно взять частные производные и приравнять их нулю:
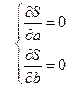
Получим систему уравнений для отыскания коэффициентов регрессии. Сколько коэффициентов присутствует в уравнении регрессии, столько будет и уравнений в этой системе.
Как известно из курса математического анализа, чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров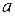 
и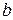 
и приравнять их к нулю. Обозначим 
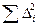через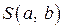 
, тогда: 
.
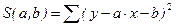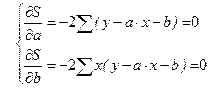
Вычислим производные и выполним преобразования полученных выражений:
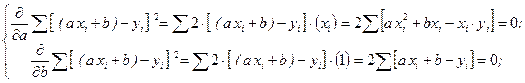
После преобразований, получим следующую систему линейных уравнений для оценки параметров 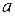и :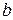
Эта система называется нормальной системой.
Если мы ее решим, то коэффициенты регрессии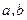 
будут найдены.
Свое название МНК получил, исходя из смыслового содержания критерия, которому должны удовлетворять полученные на его основе оценки параметров эконометрической модели: сумма квадратов значений фактической ошибки модели должна быть минимальной.
2.2. Предпосылки метода наименьших квадратов
Оценивание модели (уравнения) регрессии по методу наименьших квадратов предусматривает проверку выполнимости предпосылок МНК.