
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Парная регрессия и её виды
|
|
Парная регрессия представляет собой модель зависимости между двумя переменными – y и x, т. е. модель вида: 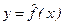 , где y – зависимая переменная (результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых:
, где y – зависимая переменная (результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых:  , где y – фактическое значение результативного признака;
, где y – фактическое значение результативного признака; 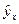 – теоретическое значение результативного признака, найденное исходя из уравнения регрессии;
– теоретическое значение результативного признака, найденное исходя из уравнения регрессии; 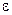 – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Модель парной регрессии также называют однофакторной эконометрической моделью, т.к. в неё входит только один признак-фактор.
Случайная величина 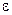 называется также возмущением. Она включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
называется также возмущением. Она включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
При построении корреляционной зависимости по данным наблюдений решаются две основные задачи:
1. Определить, какой формулой можно описать зависимость среднего значения y от x. Эту часть исследования называют спецификацией уравнения регрессии.
2. После того, как уравнение для описания подобрано, нужно оценить параметры, которые в него вошли. Данная процедура будет рассмотрена позже.
В парной регрессии выбор вида математической функции 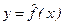 , т.е. уравнения модели, может быть осуществлен тремя методами:
, т.е. уравнения модели, может быть осуществлен тремя методами:
1) графическим;
2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи;
3) экспериментальным.
При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции.
В простейшем случае зависимость среднего значения фактора У от изменения фактора Х можно описать линейной функцией:
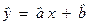
Т.е., линия регрессии – прямая линия.
 |
 |
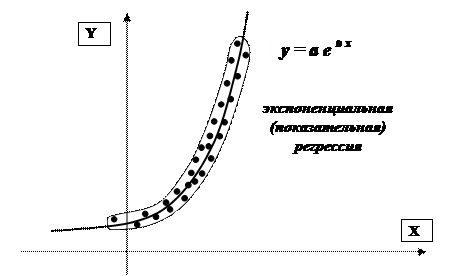
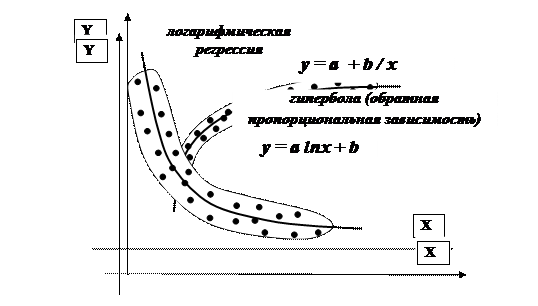
В случаях, когда корреляционное поле указывает на то, что прямая линия не подходит для описания характера зависимости, применяются более сложные виды зависимости, т.е. нелинейная регрессия. Форма этой зависимости может быть разной. В зависимости от того, какое уравнение выбирается, регрессия получает соответствующее название.
 |
 |

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.
При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии, рассчитанной при разных моделях.
Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при х должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу, то нам потребуется объем информации уже не менее 14 наблюдений.