Матричная форма МНК

Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной множественной регрессии 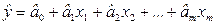параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Рассмотрим линейную модель множественной регрессии:

.

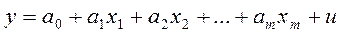Классический подход к оцениванию параметров линейной модели множественной регрессии основан на уже известном нам МНК.

При этом линейная эконометрическая модель записывается в векторно-матричной форме следующего вида:

Y=X× А+e,

где Y – вектор-столбец, состоящий из n компонент зависимой (результативной) переменной;

Х – матрица размера n ´ (m +1) (если в модели присутствует “свободный” коэффициент a ₀);

А =(a ₀, a ₁,..., a_m) – вектор-столбец параметров, состоящий из m +1-й компоненты;

e – вектор-столбец ошибки модели (остатков или отклонений), состоящий, как и вектор Y, из n компонент.

Исходными данными при оценке параметров a ₀, a ₁,..., a_m являются измеренные (наблюдаемые) значения зависимой переменной, которые можно представить в виде вектора-столбца,

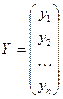
и наблюдаемые значения независимых переменных (факторов), которые объедены в матрицу следующего вида:

.

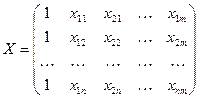В матрице Х первый столбец состоит сугубо из значений “1” является необходимым для расчета значения свободного члена (параметра a ₀) линейной эконометрической модели. Следует заметить, что расчет параметров данной модели можно производить и без столбца со значениями “1”, но в этом случае параметр a ₀ нужно будет находить отдельно. С этой целью используется формула:

,

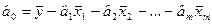где 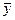, , 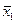,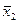..., 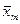– средние значения соответственно зависимой и независимых переменных (факторов).

Вектор оценок параметров Алинейной эконометрической модели в матричной форме определяется на основе следующего выражения:

А =(Х^ТХ)^–1× (Х^ТY).

Приведенное выше выражение ещё называют как оператор оценивания. При этом значения вектора А являются решением уже известной нам системы нормальных уравнений МНК. В векторно-матричной форме эта система записывается в виде:

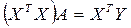
Следует отметить, что оператор оценивания может быть использован исключительно для расчета параметров линейной эконометрической модели, причем не только множественной регрессии, но и парной. В случае, если модель является нелинейной нужно предварительно преобразовать её – свести к линейной и только потом использовать выражение А =(Х^ТХ)^–1× (Х^ТY).