
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показатели тесноты связи
|
|
Формы проявления взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи.
Показатели тесноты связи дают возможность охарактеризовать зависимость вариации результативного признака от вариации признака-фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии (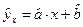 ) в качестве такого показателя выступает линейный коэффициент корреляции
) в качестве такого показателя выступает линейный коэффициент корреляции 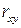 , который можно рассчитать по формуле:
, который можно рассчитать по формуле:
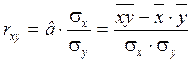 ,
,
где 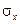 и
и 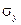 – среднеквадратическое отклонение соответственно признака-фактора и результативного признака:
– среднеквадратическое отклонение соответственно признака-фактора и результативного признака:
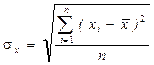 ;
; 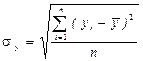 .
.
Линейный коэффициент корреляции находится в пределах: 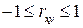 . Чем ближе абсолютное значение
. Чем ближе абсолютное значение 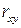 к единице, тем сильнее линейная связь между факторами (при
к единице, тем сильнее линейная связь между факторами (при 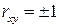 имеем строгую функциональную зависимость).
имеем строгую функциональную зависимость).
Положительное значение коэффициента корреляции говорит о положительной связи между х и у, когда с ростом одной из переменных другая тоже растет. Отрицательное значение коэффициента корреляции означает, с ростом одной из переменных другая убывает, с убыванием одной из переменной другая растет.
Теснота линейной связи между переменными может быть оценена на основании шкалы Чеддока:
| Теснота связи | Значение коэффициента корреляции при наличии: | |
| Прямой связи | Обратной связи | |
| Слабая | 0, 1–0, 3 | (–0, 3)–(–0, 1) |
| Умеренная | 0, 3–0, 5 | (–0, 5)–(–0, 3) |
| Заметная | 0, 5–0, 7 | (–0, 7)–(–0, 5) |
| Высокая | 0, 7–0, 9 | (–0, 9)–(–0, 7) |
| Очень высокая | 0, 9–1 | (–1)–(–0, 9) |
Коэффициенты регрессии (в нашем примере a) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности. Средний коэффициент эластичности 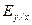 показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:
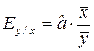
Для нелинейной или многофакторной формы зависимости теснота связи как правило определяется с помощью множественного коэффициента корреляции. Его можно вычислить как квадратный корень коэффициента детерминации, который будет рассмотрен ниже.