Примечание. Все вычисления рекомендуется выполнять строго в программе Microsoft Excel, что позволит уменьшить количество округлений и технических ошибок!

⇐ ПредыдущаяСтр 12 из 13Следующая ⇒

Например, согласно методу Гаусса разделим первое уравнение на 16, а второе – на 2510, 2.

Получим следующую систему:

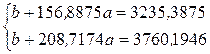Далее отнимем от второго уравнения первое (можно и наоборот – от первого уравнения второе, на итоговой результат это не повлияет).

Неизвестный параметр b сокращается, получим:

;

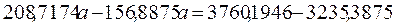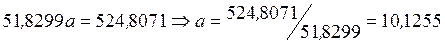Таким образом, первый неизвестный параметр мы нашли: .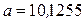

Для того, чтобы найти второй параметр нужно подставить уже известное нам значение коэффициента a в любое из уравнений предыдущей системы, например в первое. Получим:

.

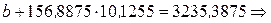
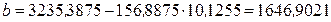Таким образом, и второй неизвестный параметр мы тоже нашли: .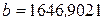

4. Записываем уравнение модели, подставив найденные значения параметров a и b в линейную форму .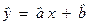

Аналитическая форма однофакторной эконометрической модели будет иметь следующий вид:

.

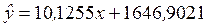Данная модель показывает зависимость между фактором (х, сумма расходов на продвижение товара) и результативной переменной (у, размер полученной прибыли)

5. Находим колонку значений 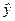(используем формулу 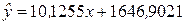и значения фактора х со второй колонки) и добавляем её к таблице 1.3. Получим следующую таблицу.

Таблица 1.4

№ п/п

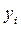
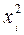
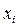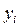
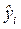
1 2 3 4 5 6

56, 2 1598, 2 3158, 44 89818, 84 2215, 93

63, 2 1768, 2 3994, 24 111750, 24 2286, 80

69, 2 1983, 2 4788, 64 137237, 44 2347, 55

75, 2 2213, 2 5655, 04 166432, 64 2408, 30

86, 2 2468, 2 7430, 44 212758, 84 2519, 68

96, 2 2733, 2 9254, 44 262933, 84 2620, 93

99, 2 3043, 2 9840, 64 301885, 44 2651, 30

122, 2 3328, 2 14932, 84 406706, 04 2884, 18

130, 2 3493, 2 16952, 04 454814, 64 2965, 18

155, 2 3583, 2 24087, 04 556112, 64 3218, 30

171, 2 3793, 2 29309, 44 649395, 84 3380, 30

208, 2 4033, 2 43347, 24 839712, 24 3754, 93

248, 2 4158, 2 61603, 24 1032065, 24 4159, 93

283, 2 4283, 2 80202, 24 1213002, 24 4514, 30

308, 2 4548, 2 94987, 24 1401755, 24 4767, 43

338, 2 4738, 2 114379, 24 1602459, 24 5071, 18

Сума 2510, 2 51766, 2 523922, 44 9438840, 64 51766, 21

6. Чтобы получить графическую интерпретацию модели, построим в системе координат x0y прямую, которая соответствует полученному уравнению модели. Это будут теоретические (расчетные, модельные) значения зависимой переменной .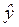

Нанесем также на той же координатной плоскости точки, которые соответствуют исходным, т.е. фактическим данным переменной y.

С этой целью используем Мастер диаграмм Microsoft Excel (пункт меню Вставка→ Диаграмма либо пиктограмма ):

Ø Выбираем тип диаграммы – точечная, вид можно оставить по умолчанию, т.е. первый.

Ø Нажимаем на кнопку " Далее", переключаемся на вкладку " Ряд" (вкладки расположены вверху окна).

Ø В случае, если в поля " Ряд" мастером уже занесены какие-либо данные –очищаем их нажимая на кнопку " Удалить" до тех пор пока она станет неактивной.

Ø Нажимаем на кнопку " Добавить" чтобы создать первый ряд данных.

Ø В поле " Имя: " вводим с клавиатуры текст фактические значения.

Ø В поле " Значения Х: " указываем столбец со значениями х со второй колонки таблицы 1.4 (выделяем диапазон значений мышкой, номер колонки и значение суммы в диапазон не входит!).

Ø В поле " Значения Y: " указываем столбец со значениями y с третьей колонки таблицы 1.4 (выделяем диапазон значений мышкой, номер колонки и значение суммы в диапазон не входит!).

Ø Нажимаем на кнопку " Добавить" чтобы создать второй ряд данных.

Ø В поле " Имя: " вводим с клавиатуры текст модельные значения.

Ø В поле " Значения Х: " указываем столбец со значениями х со второй колонки таблицы 1.4 (выделяем диапазон значений мышкой, номер колонки и значение суммы в диапазон не входит!).

Ø В поле " Значения Y: " указываем столбец со значениями 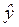с шестой колонки таблицы 1.4 (выделяем диапазон значений мышкой, номер колонки и значение суммы в диапазон не входит!).

Ø Нажимаем на кнопку " Далее", вводим с клавиатуры названия для осей Х (затраты на продвижение товара, тыс. дол. США) и Y (размер полученной прибыли, тыс. дол. США).

Ø Нажимаем на кнопку " Далее", потом на кнопку " Готово".

Ø Форматируем график: нажимаем мишкой на ряд данных с модельными значениями, заходим в меню Формат → Выделенный ряд, в появившемся окне в поле " Линия" ставим переключатель в положение " обычная", а в поле " Маркер" – в положение " отсутствует".

Ø Меняем цвета рядов данных, шрифты, заливку области построения, внешний вид линий сетки и осей по собственному усмотрению.

Результат представлен на рисунке ниже.

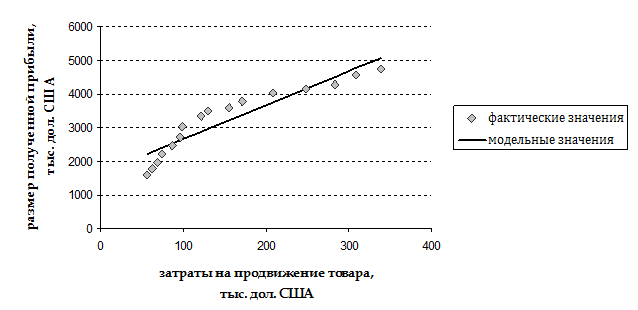
Как видно с рисунка теоретическая линия в целом достаточно хорошо отражает основные тенденции взаимосвязи между переменными х и у.

7. Находим столбец отклонений 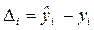и добавляем его в таблицу.

Таблица 1.5

№ п/п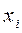

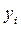
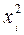
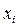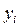
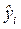
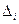
1 2 3 4 5 6 7

56, 2 1598, 2 3158, 44 89818, 84 2215, 93 -617, 73

63, 2 1768, 2 3994, 24 111750, 24 2286, 80 -518, 6

69, 2 1983, 2 4788, 64 137237, 44 2347, 55 -364, 35

75, 2 2213, 2 5655, 04 166432, 64 2408, 30 -195, 1

86, 2 2468, 2 7430, 44 212758, 84 2519, 68 -51, 48

96, 2 2733, 2 9254, 44 262933, 84 2620, 93 112, 27

99, 2 3043, 2 9840, 64 301885, 44 2651, 30 391, 9

122, 2 3328, 2 14932, 84 406706, 04 2884, 18 444, 02

130, 2 3493, 2 16952, 04 454814, 64 2965, 18 528, 02

155, 2 3583, 2 24087, 04 556112, 64 3218, 30 364, 9

171, 2 3793, 2 29309, 44 649395, 84 3380, 30 412, 9

208, 2 4033, 2 43347, 24 839712, 24 3754, 93 278, 27

248, 2 4158, 2 61603, 24 1032065, 24 4159, 93 -1, 73

283, 2 4283, 2 80202, 24 1213002, 24 4514, 30 -231, 1

308, 2 4548, 2 94987, 24 1401755, 24 4767, 43 -219, 23

338, 2 4738, 2 114379, 24 1602459, 24 5071, 18 -332, 98

Сума 2510, 2 51766, 2 523922, 44 9438840, 64 51766, 21 -0, 02

Примечание. Значение суммы по столбцу должно быть как можно ближе к нулю и свидетельствует о правильности выполненных расчетов. По умолчанию программа Microsoft Excel очень маленькие числа записывает в экспоненциальном формате.

Например, запись-8, 37E-12 в обычном формате (–0, 00000000000837) будет занимать очень много места, поэтому можно оставить это число в экспоненциальной форме. В тоже время запись 4, 368E-05 уже не такая длинная, поэтому её формат можно изменить на обычный (0, 00004368).

Замена формата числа производится через пункт меню Формат → Ячейки во вкладке " Число". Предварительно требуемая ячейка (диапазон ячеек) должна быть выделена мышкой.

8. Находим дисперсии отклонений и результативного признака. При этом пользуемся функцией ДИСП категории " Статистические".

Дисперсия результативного признака рассчитывается по третьей колонке таблицы 1.5 (выделяем диапазон значений мышкой, номер колонки и значение суммы в диапазон не входит!) и в нашем случае равна .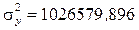

Дисперсия отклонений рассчитывается по седьмой колонке таблицы 1.5 (выделяем диапазон значений мышкой, номер колонки и значение суммы в диапазон не входит!) и в нашем случае равна .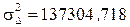

9. Рассчитываем коэффициент детерминации за формулой:

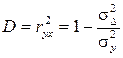В нашем случае:

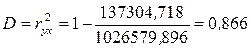Полученное значение коэффициента детерминации является достаточно большим и характеризует правильность подбора линейной функции для построения эконометрической модели.

В 86, 6% случаев изменения х приводят к изменению y. Остальные 13, 4% изменения y объясняются факторами, неучтенными в модели.

10. Находим множественный коэффициент корреляции как квадратный корень с коэффициента детерминации. Для этого используем функцию КОРЕНЬ категории " Математические".

В нашем случае, поскольку модель однофакторная, то множественный коэффициент корреляции совпадает с обычным линейным коэффициентом корреляции, который равен 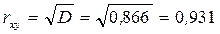или 93, 1%.

На основании шкалы Чеддока можно сделать вывод, что связь между х (затраты на продвижение товара) и у (размер полученной прибыли) является очень высокой.

⇐ Предыдущая 4 5 6 7 8 9 10 111213 Следующая ⇒

Поделиться с друзьями:

mylektsii.su - Мои Лекции - 2015-2024 год. (0.01 сек.)Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав Пожаловаться на материал