Пример выполнения

Пусть две последних цифры зачетной книжки N=00.

Будем считать, что между факторами (общие расходы и размер семьи) и результативной переменной (размер полученной прибыли) существует линейная зависимость. В таком случае мы имеем линейную многофакторную модель (модель множественной регрессии) общего вида (см. § 3.2):

,

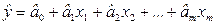где – неизвестные параметры модели (коэффициенты, которые нам нужно рассчитать).

Конкретно для нашего задания формула эконометрической модели будет выглядеть так:

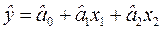
Рассчитывать (оценивать) параметры нашей модели будем при помощи МНК в матричной форме следующего вида:

Y=X× А+e,

где Y – вектор-столбец, состоящий из n (в нашем случае – 16) компонент зависимой (результативной) переменной;

Х – матрица размера n ´ (m +1) (в нашем случае 16х3), состоящая их компонент независимых переменных;

А =(a ₀, a ₁,..., a_m) – вектор-столбец параметров, состоящий из m +1-й компоненты (в нашем случае – из 3);

e – вектор-столбец ошибки модели (остатков или отклонений), состоящий, как и вектор Y, из n компонент.

Напомним, что оператор оценивания параметров линейной эконометрической модели в матричной форме имеет вид:

А = (Х^ТХ)^–1× (Х^ТY).

Процедуру оценивания параметров эконометрической модели целесообразно разбить на следующие шаги.

1) Записываем матрицу независимых переменных Х:

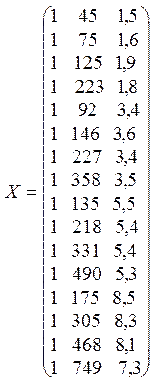
В Microsoft Excel матрица записывается как обычная таблица – каждое число в отдельной ячейке:

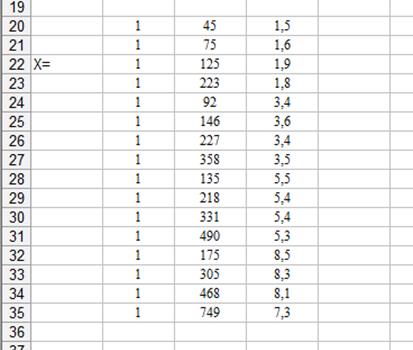
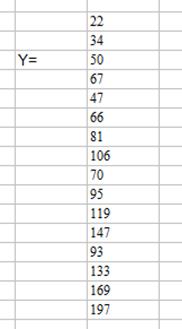
2) Записываем вектор-столбец зависимой (результативной) переменной Y:

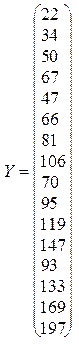
3) Находим транспонированную матрицу к матрице независимых переменных Х, т.е. матрицу Х^Т.

При этом рекомендуется копирование с использованием пункта контекстного меню " Специальная вставка", проставив галочку напротив пункта " транспонировать" (предварительно нужно выделить цифры матрицы Х, нажать пункт контекстного меню " копировать" и проставить курсор в незанятую ячейку, после чего вызывать меню " Специальная вставка").

4) Находим произведение матриц Х^ТХ. При этом используем функцию Microsoft Excel МУМНОЖ категории " Математические".

Алгоритм использования функции МУМНОЖ следующий:

- Выделяем на листе блок свободных ячеек, в котором будет размещен результат произведения матриц (в нашем случае размеры этого блока 3х3);

- Вызываем функцию МУМНОЖ;

- В окне " Аргументы функции" ставим курсор в поле " Массив1" выделяем мышкой цифры матрицы Х^Т;

- Ставим курсор в поле " Массив2" выделяем мышкой цифры матрицы Х;

- Одной рукою зажимаем на клавиатуре комбинацию клавиш Ctrl+Shift, другой рукой нажимаем мышкой на клавишу ОК (второй способ – нажатие на клавиатуре комбинации клавиш Ctrl+Shift+Enter, тогда клавишу ОК нажимать не требуется).

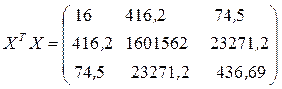
5) Находим произведение матриц Х^ТY. Используем функцию МУМНОЖ. В этом случае диапазон свободных ячеек будет иметь размеры 3х1:

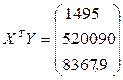
6) Находим матрицу, обратную к матрице Х^ТХ. Приэтом пользуемся функцией МОБР категории " Математические". Диапазон свободных ячеек будет иметь такие же размеры, как и матрица Х^ТХ. Не забываем об нажатии клавиш Ctrl+Shift+ОК или Ctrl+Shift+Enter.

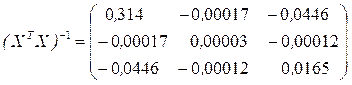
7) Находим произведение матриц (Х^ТХ)^–1× (Х^ТY), т.е оператор оценивания 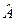. Используем функцию МУМНОЖ. Диапазон свободных ячеек будет иметь размеры 3х1. В поле " Массив1" указываем цифры матрицы (Х^ТХ)^–1, а в поле " Массив2" – матрицу (Х^ТY).

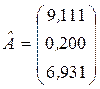
Итак найденные в матричной форме оценки параметров следующие: 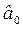= 9, 1111; 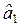= 0, 2; 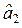= 6, 931.

Таким образом, эконометрическая модель зависимости затрат на питание от общих расходов и размера семьи будет иметь вид:

.

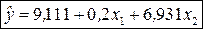
8) Выполняем проверку правильности расчета параметров эконометрической модели. При этом используем функцию ЛИНЕЙН категории " Статистические". Алгоритм будет следующий:

- Выделяем мышкой на листе блок свободных ячеек размером 5х3 (число строк (5) – стандартное значение, т.е. одинаковое всегда, число столбцов (3) определяется количеством оцениваемых параметров);

- Вызываем функцию ЛИНЕЙН;

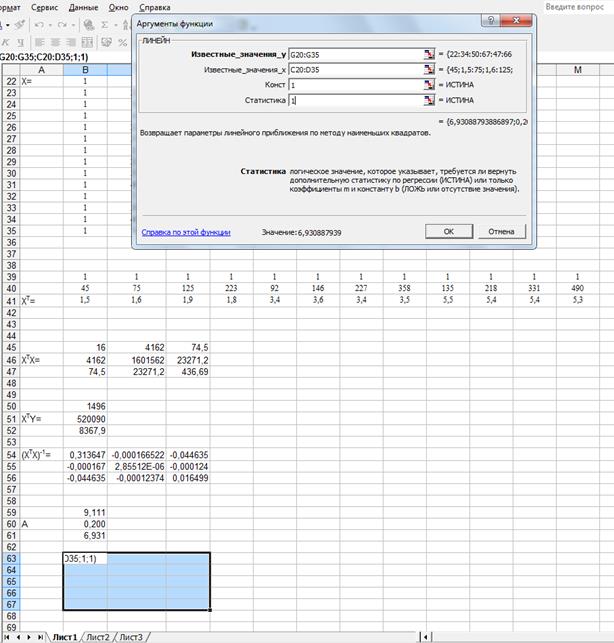
- В поле " Известные_значения_у" указываем цифровые значения вектора-столбца зависимой (результативной) переменной Y, а в поле " Известные_значения_х" – цифровые значения матрицы Х (указываем только значения, которые соответствуют переменным х₁ и х₂, первый столбец (тот, что с единичками) не трогаем!);

- В поле " Конст" пишем 1 либо текст " Истина" (это позволит рассчитать свободный член );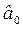

- В поле " Статистика" тоже пишем 1 либо текст " Истина" (это позволит рассчитать дополнительные коэффициенты качественных характеристик нашей модели);

- Нажимаем клавиши Ctrl+Shift+ОК или Ctrl+Shift+Enter.

Регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента	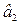Значение коэффициента	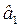Значение коэффициента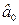
Среднеквадратическое отклонение	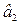Среднеквадратическое отклонение	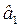Среднеквадратическое отклонение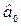
Коэффициент детерминации D (R2)	Среднеквадратическое отклонение y
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

В нашем случае получены такие значения:

Таким образом, значения коэффициентов эконометрической модели 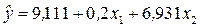рассчитаны правильно.

Выводы

1. С помощью МНК (в матричной форме) мы нашли уравнение эконометрической модели, которая показывает зависимость затрат на питание от общих расходов и размера семьи и относится к классу линейных многофакторных эконометрических моделей.

2. Коэффициенты уравнения 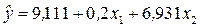имеют следующее экономическое обоснование. Когда при всех других одинаковых условиях общие расходы увеличиваются (уменьшаются) на 1 дол. США, то результативная переменная (расходы на питание) также увеличивается (уменьшается) на 0, 2 дол. США. Если размер семьи увеличивается (уменьшается) на 1 чел., то расходы на питание также увеличивается (уменьшается) на 6, 93 дол. США.

Параметр 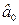с формальной точки зрения показывает следующее: если значение двух независимых переменных (общие расходы и размер семьи) равно нулю, то расходы на питание = 9, 11 дол. США). Очевидно, что в данной модели этот коэффициент экономического смысла не имеет и служит в роли начальной точки отсчета.

3. Полученное с помощью функции ЛИНЕЙН высокое значение коэффициента детерминации (0, 9845 или 98, 45%) характеризует правильность подбора линейной функции для построения эконометрической модели, т.е. модель в целом является адекватной.

4. Фактическое значение 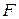-критерия Фишера (413, 826) гораздо больше табличного значения, что подтверждает значимость уравнения регрессии в целом.

5. Полученные значения среднеквадратических отклонений (стандартных ошибок) коэффициентов эконометрической модели не являются слишком большими. За исключением коэффициента 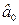среднеквадратические отклонения других параметров существенно меньше по сравнению с абсолютными значениями самых параметров, таким образом их относительная ошибка будет в пределах допустимых значений: для параметра 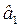– в пределах 5, 6% (; для параметра – в пределах 12, 2% (.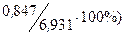

РЕКОМЕДОВАННАЯ ЛИТЕРАТУРА

1. Бородич С.А. Вводный курс эконометрики: Учебное пособие. – Минск: БГУ, 2000. – 354 с.

2. Горбатков С.А. Эконометрика: авторский курс лекции. – Уфа: Филиал ВЗФЭИ в г. Уфа, 2008.

3. Замков О.О. Математические методы в экономике: Учебник / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных / Под общ. ред. А.В. Сидоровича. – 4-е изд., стереотип. – М.: Издательство «Дело и Сервис», 2004. – 368 с.

4. Клебанова Т.С., Дубровина Н.А., Раевнева Е.В. Эконометрия: Учебное пособие. – 2-е изд., испр. – Харьков: ИД «ИНЖЭК», 2005. – 160 с.

5. Лугінін О.Є., Білоусова С.В., Білоусов О.М. Економетрія: Навч. посібник. – К.: Центр навчальної літератури, 2005. – 252 с.

6. Лук’яненко І.Г., Краснікова Л.І. Економетрика: Практикум з використанням комп’ютера. – К.: Товариство „Знання”, 1998. – 220 с.

7. Наконечний С.І., Терещенко Т.О., Романюк Т.П. Економетрія: Підручник. – Вид. 3-тє, доп. та перероб. – К.: КНЕУ, 2004. – 520 с.

8. Орлов А.И. Эконометрика: Учебное пособие для ВУЗов. – М.: ЭКЗАМЕН, 2007.

9. Практикум по эконометрике: Учебное пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2006. – 344 с.

10. Шалабанов А.К., Роганов Д.А. Практикум по эконометрике с применением MS Excel. Линейные модели парной и множественной регрессии. – Казань: ТИСБИ, 2008. – 53 с.

Навчально-методичне видання

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

Тиражування на різографі – Ю.М. Рубан

Здано до тиражування 25.01.2014. Підписано до друку 27.01.2014. Папір газетний. Гарнітура Times. Формат 60х84 1/16. Ум. друк. арк. 3, 0. Тираж 100 прим.

РВЛ КНТУ. Зам. № /2014.