Доказательство

Случай 1. Транспонируемые числа стоят в перестановке рядом, т.е. она имеет вид (..., k, p,...), здесь многоточием (...) отмечены числа, которые при транспозиции остаются на своих местах. Транспозиция превращает ее в перестановку вида (..., p, k,...). В этих перестановках каждое из чисел k, р составляет одни и те же инверсии с числами, остающимися на местах. Если числа k и p ранее не составляли инверсии, (т.е. k < р), то в новой перестановке появится еще одна инверсия и число инверсий увеличится на одну; если же k и р составляли инверсию, то после транспозиции число инверсий станет меньше на одну. В любом случае четность перестановки меняется.

Случай 2. Между транспонируемыми числами k и р находится s чисел, т.е. перестановка имеет вид (..., k, j ₁, j ₂,..., j_s, p,...). В этом случае потребуется 2 s + l транспозиций соседних чисел: s транспозиций, чтобы поменять последовательно местами k с j ₁, k с j ₂,..., k с j_s, и s + 1 транспозиций, чтобы поменять местами р с k, р с j_s, р с j_{s- 1},..., p c j ₁.

Таким образом, в силу доказанного случая 1, четность перестановки меняется нечетное число раз, следовательно, исходная перестановка и перестановка, полученная в результате транспозиции, имеют разные чётности.

Для сокращения записи перестановки будем обозначать одним символом, например: 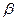, т.е. 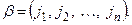Обозначим через n (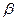) число инверсий в перестановке .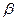