
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определители. Рассмотрим квадратную матрицу порядка n.
|
|
Рассмотрим квадратную матрицу 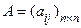 порядка n.
порядка n.
Определителем или детерминантом n -го порядка матрицы А называется число
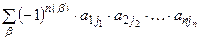 ,
,
где сумма вычисляется по всем перестановкам вторых индексов.
Обозначения определителя: 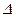 , det A, или в полной записи:
, det A, или в полной записи:
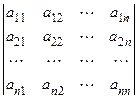 .
.
Таким образом, по определению
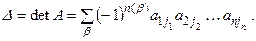 (1.3)
(1.3)
В соответствии с доказанным утверждением 1.1, в правой части формулы (1.3) n! слагаемых, причем n! / 2 слагаемых со знаком «+» и n! /2 со знаком «–», так как если
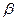 – четная перестановка, то
– четная перестановка, то 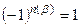 , а если
, а если 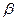 – нечетная, то
– нечетная, то 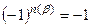 . При этом каждое из слагаемых является произведением n чисел, которые расположены в разных строках и разных столбцах матрицы.
. При этом каждое из слагаемых является произведением n чисел, которые расположены в разных строках и разных столбцах матрицы.
Используя определение определителя порядка n, получим формулы для вычисления определителей 2-го и 3-го порядка.
При n = 2 перестановок вторых индексов будет 2! = 2, одна четная – (12) и одна нечетная (21), следовательно:
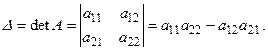 (1.4)
(1.4)
При n = 3 перестановок вторых индексов – 3! = 6. Четные: (123) (0 инверсий), (231) (2 инверсии), (312) (2 инверсии). Нечетные: (321) (3 инверсии), (132) (1 инверсия). (213) (1 инверсия). Следовательно:
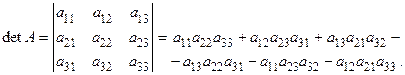 (1.5)
(1.5)
Для запоминания знаков слагаемых и сомножителей в каждом слагаемом полезно запомнить следующее мнемоническое правило.