Теорема 1.1 (Крамера)

Если 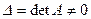, то система совместна, имеет единственное решение, которое определяется равенствами

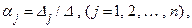(1.12)

где 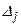– определитель матрицы, которая получается из матрицы системы заменой j -го столбца столбцом, составленным из свободных членов системы b ₁, b ₂, …, b_n.

Доказательство. С помощью элементарных преобразований приведем систему к простейшему виду, для чего при каждом 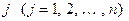умножим i -е уравнение на А_ij и сложим левые и правые части всех полученных уравнений

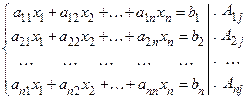
в результате получим систему уравнений, эквивалентную исходной, в которой j -е уравнение имеет вид:

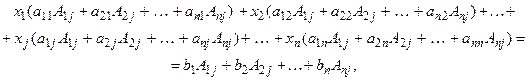
или

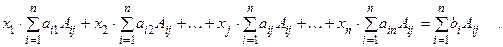
По теореме аннулирования (формула (1.10))

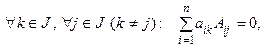
а по формуле (1.9) (при k = j)

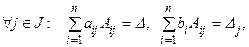
т.е. j -е уравнение в системе имеет вид 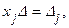откуда получаем решение:

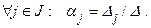
Равенства (1.12) называются формулами Крамера.

Например, для системы трех уравнений с тремя неизвестным можно записать: