Ранг матрицы

Рассмотрим прямоугольную матрицу 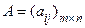. Выберем в матрице А произвольно k строк сномерами i ₁, i ₂, …, i_k и k столбцов с номерами j ₁, j ₂ ,..., j_k, 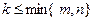. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу А_k порядка k.

Определитель матрицы А_k называется минором k -гo порядка (минором порядка k) и обозначается 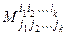или, когда не важно, какие именно строки и столбцы выбраны, обозначается M_k, т.е. по определению M_k = det А_k. Например, если

и выбраны строки c номерами i ₁ = 1, i ₂ = 3 и столбцы с номерами j ₁ = 2, j ₂ = 4, то

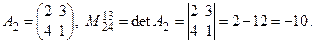
Число миноров второго порядка для этой матрицы равно 18.

Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или r _A.

Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.

Пример 1.2. Найти ранг матрицы:

.

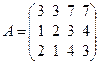Решение. Здесь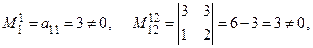

,

следовательно rаng А = 2.

Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.

Элементарные преобразования матрицы:

1) перестановка (транспозиция) строк (столбцов) матрицы;

2) умножение всех элементов отроки (столбца) матрицы на действительное число ;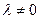

3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.