Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Гаусса. Теорема Кронекера-Капелли
|
|
Рассмотрим систему линейных уравнений (1.11). К матрице системы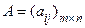 
допишем справа столбециз свободных членов системы b 1, b 2, ..., bm, получим новую матрицу, которая называется расширенной матрицей системы и обозначается: 
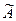, т.е.
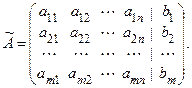
Элементарным преобразованиям расширенной матрицы системы (cм. разд. 1.7) соответствуют эквивалентные преобразования системы линейных уравнений (1.11)
(см. разд. 1.4), поэтому решение системы с помощью эквивалентных преобразований можно заменить на приведение расширенной матрицы с помощью элементарных преобразований к более простой форме. Метод Гаусса состоит из двух частей – прямого и обратного хода. Идея прямого хода метода – с помощью элементарных преобразований привести расширенную матрицу к виду, в котором матрица системы имеет трапециевидную форму.