Обратный ход метода Гаусса

Шаг 1. Из последнего уравнения системы (1.15) находим у_r, подставив вместо свободных неизвестных произвольные числа 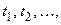t_n-r:

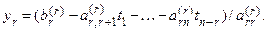
Шаг 2. Подставляем найденный у_r в предпоследнее уравнение и находим y_{r -1}:

...

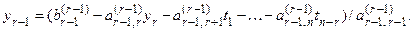
Шаг r. Подставляем найденные у_r, …, у ₂ в первое уравнение находим у ₁:

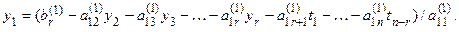
В результате, получаем решение системы (1.11), в котором базисные переменные выражены через свободные переменные.

Замечание. Из доказательства теоремы Кронекера-Капелли следует, что:

· если rang A = rang 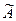= n, то система совместна и имеет единственное решение;

· если rang A = rang 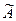< n, то система совместна и имеет бесконечное множество решений;

· если rang A < rang 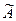, то система несовместна.

Пример 1.3. Решить систему линейных уравнений:

.

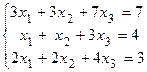Решение. Приведем расширенную матрицу системы:

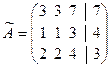
к трапециевидной форме. Поменяем местами первую и вторую строки матрицы, затем умножим элементы первой строки на –3 и прибавим к элементам второй сроки, элементы первой строки умножим на –2 и прибавим к элементам третьей строки, получим:

Матрица 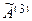имеет трапециевидную форму, причем в полученных матрицах по две ненулевых, строки, т.е. rang A = rang 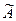= 2, следовательно, по теореме Кронекера-Капелли система совместна и имеет бесконечное множество решений. Полученной матрице соответствует система уравнений, эквивалентная исходной:

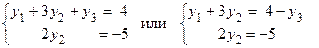
где y ₁ = x ₁, y ₂ = x ₃, y ₃ = x ₂, (второй и третий столбцы в расширенной матрице менялись местами). Пусть у ₃ = t, тогдаиз второго уравнения находим у ₂ = 2, 5 и, подставляя у ₂ в первое уравнение, получим у ₁ = –3, 5 – t. Таким образом, решением данной системы уравнений будут 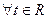: х ₁ = –3, 5 – t, х ₂ = t, x ₃ = 2, 5.