Доказательство. Необходимость. Так как система векторов линейно зависима, то такие, что

Необходимость. Так как система векторов линейно зависима, то 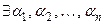такие, что

.

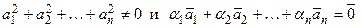Пусть, например, а_i 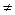0, тогда

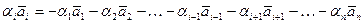
или ,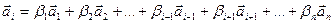

где .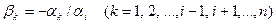

Таким образом, вектор 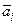является линейной комбинацией остальных n – 1 векторов.

Достаточность. Пусть, например,

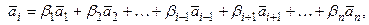
перенесем 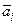, в правую часть равенства и получим нетривиальную линейную комбинацию векторов (так как 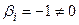), равную .

Базисом в линейном пространстве L называется любая упорядоченная система векторов, обладающая следующими свойствами:

· она линейно независима;

· любой вектор из L является линейной комбинацией векторов этой системы.

Пусть таких векторов в системе n штук. Обозначим эти векторы: 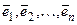. Коэффициенты линейной комбинации векторов, о которой идет речь в определении (свойство б), называются координатами вектора в базисе 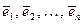, т.е., если 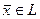, то

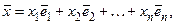
и тогда 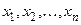– координаты вектора 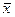в базисе 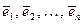. Обозначим через Х матрицу-столбец, состоящую из координат вектора 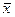, через e – матрицу-строку, состоящую из векторов базиса 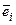, тогда