Из определения скалярного произведения и формул (2.5), (2.9) следует, что

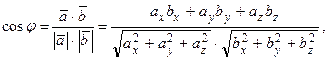(2.10)

где 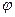угол между векторами .

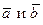2) Вычисление проекции одного вектора на другой

Из равенств (2.8) находим:

.

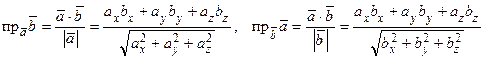3) Условие перпендикулярности векторов

Используя свойство 1^о и формулу (2.9), получаем:

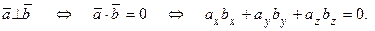
Векторное произведение векторов и его свойства

Упорядоченная тройка векторов 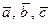называется правой, если кратчайший поворот первого вектора ко второму видениз конца третьего вектора против часовой стрелки, в противном случае тройка векторов называется левой.

Векторным произведением двух векторов 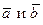называется третий вектор 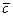, удовлетворяющий условиям:

а) длина вектора 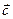вычисляется по формуле:

,

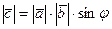где 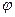угол между векторами .

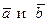Б) вектор 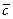перпендикулярен векторам ;

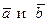в) тройка векторов 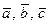правая.

Обозначение: 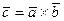или .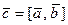

Свойства векторного произведения векторов

1°. 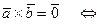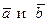– коллинеарные векторы;

2°. ;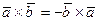

3°. ;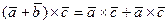

4°. 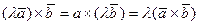.