Смешанное произведение векторов и его свойства

Пусть 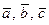– три произвольных вектора.

Три вектора называются компланарными, если они параллельны одной плоскости, т.е., будучи приведены к одному началу, лежат в одной плоскости.

Смешанным произведением векторов 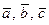называется число равное скалярному произведению векторного произведения векторов 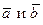на вектор 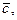т.е. 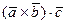Геометрический смысл смешанного произведения определяется следующей теоремой.

Теорема 2.1. Смешанное произведение 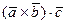равно объему параллелепипеда V, построенного на векторах 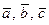, взятому со знаком " +", если тройка векторов 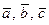правая, и со знаком " –", если тройка векторов 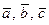левая. Если векторы 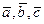компланарны, то смешанное произведение рано нулю, т.е.

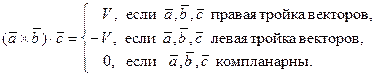
Доказательство

Пусть 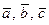– некомпланарные векторы, образующие правую тройку. Обозначим через V объем параллелепипеда, построенного на векторах 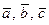, через S – площадь параллелограмма, построенного на векторах , через h – высоту параллелепипеда, опущенную из конца вектора 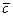, через 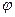– угол между векторами, 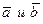, через
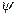– угол между векторам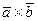и и 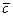(рис. 2.10). Тогда по определению скалярного и векторного произведений векторов находим:

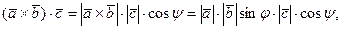
но .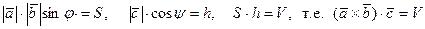

Пусть 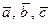– некомпланарные векторы, образующие левую тройку, тогда векторы 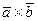и 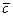образуют угол, равный 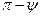, при этом 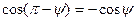, следовательно:

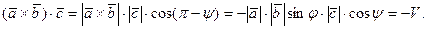
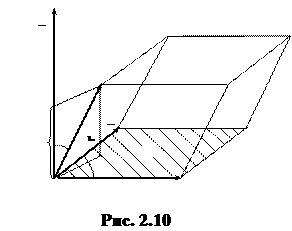Пусть 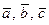компланарны. Если 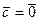, то утверждение очевидно. Пусть 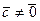, тогда либо 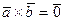(если векторы 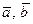коллинеарны) и 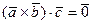, либо и тогда .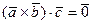

Верно и обратное последнему утверждение, т.е., если 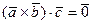, то векторы 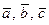компланарны. Действительно, если 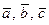некомпланарны, то по теореме 2.1 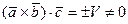, что противоречит условию .

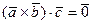Теорема 2.2. В смешанном произведении векторов знаки векторного и скалярного произведений можно поменять местами, т.е.

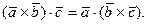
Доказательство. По свойству 2° скалярного произведения имеем:

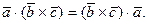
По теореме 2.1

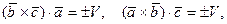(2.12)

причем тройки векторов 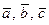и 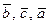одинаково ориентированы, т.е. если 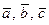правая тройка, то и 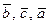правая тройка, если 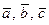левая тройка, то и 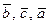левая тройка. Следовательно, в правых частях равенств (2.12) знаки одинаковые, т.е.

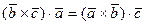или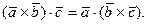

Так как справедлива теорема 2.2, смешанное произведение обозначают символом .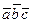

Найдем выражение смешанного произведения векторов через координаты сомножителей. Пусть

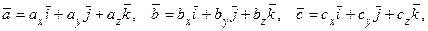
тогда по формулам (2.9), (2.11) находим: