Связь между матрицами одного и того же линейного оператора в разных базисах

Если в базисе 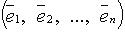линейный оператор 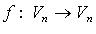имеет матрицу A, в базисе 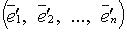- матрицу B, а S - матрица перехода от первого базиса ко второму, то

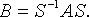
Произведение и сумма линейных операторов

Если f и g - линейные операторы пространства 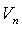с матрицами A и B в базисе 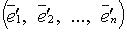, то операторы произведения 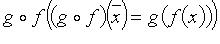и суммы 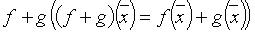- линейные и имеют в том же базисе матрицы BA и A + B соответственно.

Оператор, обратный данному линейному оператору

Линейный оператор 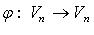называется обратным линейному оператору 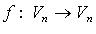, если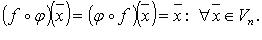

Обозначение: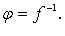

Для существования 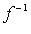необходимо и достаточно, чтобы f был невырожденным оператором. Если A - матрица оператора f в некотором базисе, то оператор 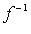в том же базисе имеет матрицу .

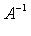Ядро и область значений линейного оператора

Ядро оператора: 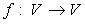- множество, обозначаемое Ker f:

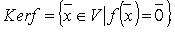
Область значений (образ) оператора 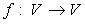- множество, обозначаемое Im f:

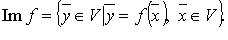
Множества Ker f и Im f являются подпространствами пространства V.

Ранг оператора 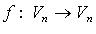(обозначение: dim Im f) - ранг матрицы A линейного оператора f,

dim Im f = rank A.

Дефектом оператора 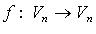называют dim Ker f,

dim Im f + dim Ker f = n.