Линейная комбинация векторов

Линейной комбинацией векторов 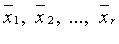называют вектор

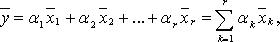
где 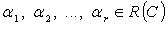- коэффициенты линейной комбинации. Если 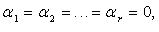комбинация называется тривиальной, если 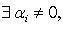- нетривиальной.

Линейная зависимость и независимость векторов

Система 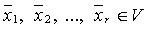линейно зависима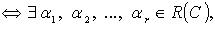 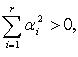что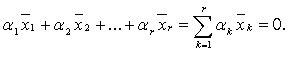

Система 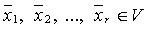линейно независима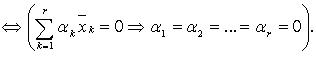

Критерий линейной зависимости векторов

Для того чтобы векторы 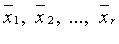(r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

Размерность линейного пространства

Линейное пространство V называется n -мерным (имеет размерность n), если в нем:

1) существует n линейно независимых векторов;

2) любая система n + 1 векторов линейно зависима.

Обозначения: n = dim V; .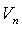

Базис пространства 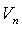. Координаты вектора

Базис - любая упорядоченная система 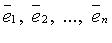из n линейно независимых векторов пространства .

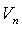Обозначение: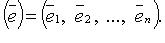

Для каждого вектора 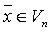существуют числа 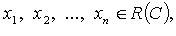такие что

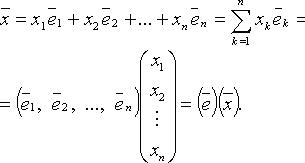
Числа 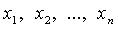называются координатами вектора в базисе (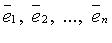) (определяются однозначно), X = (x) - координатный столбец вектора в этом базисе. Употребляется запись: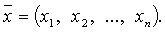

Справедливы формулы: