Линейные векторные пространства

Определение линейного пространства

Пусть V - непустое множество (его элементы будем называть векторами и обозначать 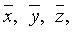...), в котором установлены правила:

1) любым двум элементам 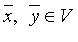соответствует третий элемент 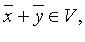называемый суммой элементов 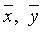(внутренняя операция);

2) каждому 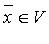и каждому 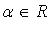отвечает определенный элемент 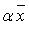(внешняя операция).

Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:

I.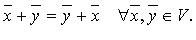

II.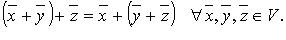

III. 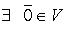(нулевой элемент, такой, что ).

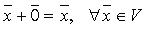IV. 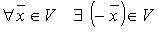(элемент, противоположный элементу ), такой, что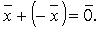

V.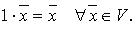

VI.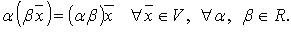

VII.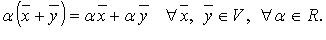

VIII.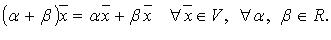
Аналогично определяется комплексное линейное пространство (вместо R рассматривается C).

Подпространство линейного пространства

Множество 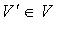называется подпространством линейного пространства V, если:

1)

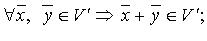
2)