Координаты вектора. Координатная запись вектора

Рассмотрим декартову систему координат, т.е. три взаимно перпендикулярных, пересекающихся в точке 0 оси 0 х, 0 у, 0 z. Пусть 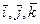– единичные направляющие векторы этих осей и 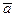– произвольный вектор. Покажем, что векторы 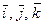образуют базис. Отложим вектор 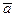от начала координат, пусть М – конец вектора 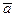, т.е. 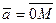(рис. 2.7). Обозначим 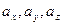– проекции вектора 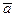на оси координат, – проекции точки М на оси координат, 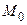– проекцию точки М на плоскость 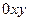. Тогда, по определению произведения вектора на число, получаем (рис. 2.7):

.

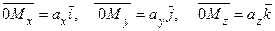По определению сложения и равенства векторов

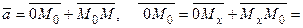
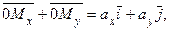
следовательно:

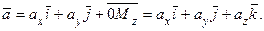
Проекции вектора на оси координат называются координатами вектора. Таким образом, координатная запись вектора имеет вид:

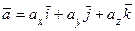. (2.4)

Откуда следует, что 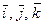– базис.

Довольно часто вектор задается перечислением его координат, т.е. запись имеет вид: 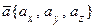или 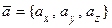(первая запись является более строгой, но чаще используется вторая).

Пусть 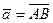, проекция точки А на ось 0 u имеет координату 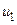, а проекция точки В – координату 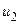, тогда по определению проекции вектора на ось

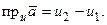
Следовательно, если

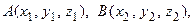
то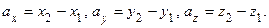

Из доказанных в разд. 2.2 свойств проекций вектора на ось получаем правила сложения и умножения вектора на число в координатной форме:

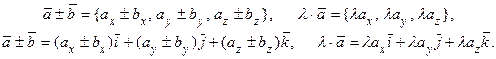
По теореме Пифагора находим длину вектора (рис. 2.7):

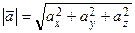(2.5)

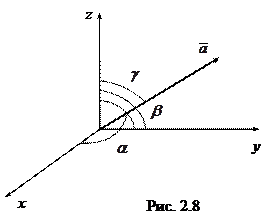Из определения произведения вектора на число следует, что если 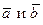ненулевые коллинеарные векторы, то 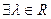такое, что 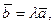или

.

Отсюда получаем условие коллинеарности векторов, заданных своими координатам:

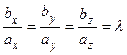. (2.6)

Пусть 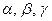– углы, которые вектор 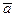составляет с осями координат (рис. 2.8), тогда по формуле (2.1)

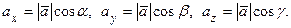
Возведя в квадрат эти равенства и сложив их, получим:

.

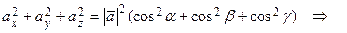
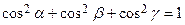Кроме того, 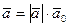, т.е.

,

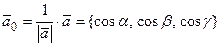где 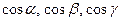– направляющие косинусы вектора 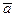. Координаты единичного вектора равны направляющим косинусам.