Линейные пространства

Множество L называется линейным пространством, а его элементы – векторами (будем обозначатьих с чертой сверху), если:

1) определена операция сложения, которая 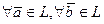ставит в соответствие элемент 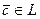, называемый суммой, который обозначается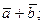

2) определена операция умножения на число, которая 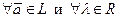ставит в соответствие элемент 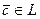, называемый произведением вектора 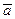на число 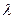, который обозначается ;

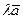3) 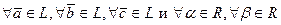выполняются следующие аксиомы:

1°. ;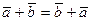

2^о. ;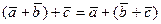

3°. существует единственный вектор 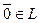такой, что 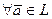справедливо равенство: ;

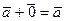4°. 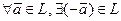такой, что; ;

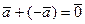5°. ;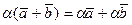

6°. ;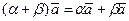

7°. ;

8°. .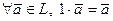

Вектор 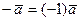называется противоположным вектору 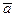. Вектор называется нулевым вектором. Сумма векторов 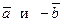называется разностью и обозначается: .

Выражение вида 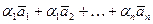называется линейной комбинацией векторов 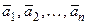. Линейная комбинация векторов называется тривиальной, если

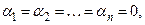
и нетривиальной, если 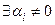. Далее будем использовать факт, что

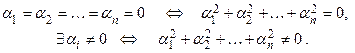
Система векторов 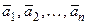называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору.

Если равенство нулевому вектору возможно лишь для тривиальной линейной комбинации, то система векторов 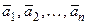называется линейно независимой.

Таким образом:

система векторов линейно зависима, если 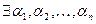такие, что

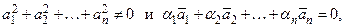
система векторов линейно независима, если 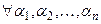справедливо

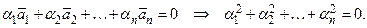
Утверждение 1.5. Система из n (n > 1) ненулевых векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов является линейной комбинацией остальных.