Линейные преобразования евклидова пространства

Ортогональные операторы

Линейный оператор 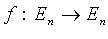называется ортогональным, если

Для того чтобы оператор 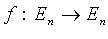был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.

Ортогональные операторы и только они сохраняют длину вектора, т. е.

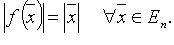
Сопряженные операторы

Оператор 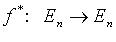называется сопряженным линейному оператору 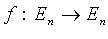, если

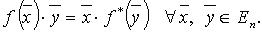
Оператор также является линейным оператором. Если f в некотором ортогональном базисе имеет матрицу A, то в этом базисе оператор имеет матрицу .

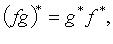
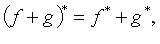
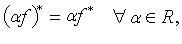
Свойства сопряженных операторов: 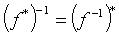(f - невырожденный).

Самосопряженные операторы

Линейный оператор 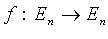называется самосопряженным (симметрическим), если

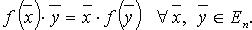
Для самосопряженного оператора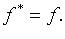

Оператор 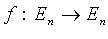является самосопряженным тогда и только тогда, когда его матрица в некотором ортонормированном базисе симметрическая.

Свойства самосопряженных операторов: 1) самосопряженный оператор имеет только действительные собственные числа; 2) всякий самосопряженный оператор является оператором простой структуры; 3) для всякого самосопряженного оператора существует ортонормированный базис, состоящий из собственных векторов этого оператора.