
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Системы линейных уравнений. Формулы Крамера
|
|
Система m уравнений с n неизвестными х 1, х 2,..., хn вида:
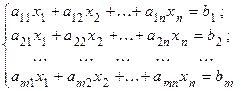 (1.11)
(1.11)
называется системой линейных уравнений.
Если b 1 = b 2 =... = bm = 0, то система называется однородной, и неоднородной в противном случае.
Набор чисел 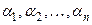 называется решением системы, если при подстановке этих чисел в уравнения системы (1.11) вместо неизвестных все уравнения обращаются в верные числовые равенства.
называется решением системы, если при подстановке этих чисел в уравнения системы (1.11) вместо неизвестных все уравнения обращаются в верные числовые равенства.
Если существует хотя бы одно решение системы, то она называется совместной, и несовместной, если решений нет.
Система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если решений более одного.
Коэффициенты при неизвестных aij (i = 1, 2, …, m; j = 1, 2, …, n) образуют матрицу 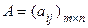 , которая называется матрицей системы.
, которая называется матрицей системы.
Две системы называются эквивалентными, если множества их решений совпадают.
Преобразования, переводящие систему в эквивалентную ей, называются эквивалентными.
Многие методы решения систем основываются на эквивалентных преобразованиях с целью получения систем более простого вида. Перечислим основные эквивалентные преобразования:
а) перестановка двух уравнений в системе;
б) умножение уравнения на число, не равное нулю;
в) прибавление к уравнению системы другого уравнения, умноженного на некоторое число 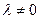 ;
;
г) перестановка слагаемых в левых частях уравнений.
При исследовании и решении систем линейных уравнений возникают следующие основные задачи:
· определить, совместна ли данная система;
· в случае совместности системы определить число решений;
· указать способ, с помощью которого можно найти все решения.
Рассмотрим, прежде всего, частный случай системы (1.11), когда число уравнений совпадает с числом неизвестных, т.е. m = n. В этом случае матрица системы А является квадратной порядка n и ответ на все поставленные вопросы дает следующая теорема.