Плоскость в пространстве

Пусть в пространстве задана прямоугольная система координат: 0 – начало координат, 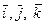– единичные направляющие векторы осей координат, соответственно 0 х, 0 у и 0 z. Рассмотрим в пространстве произвольную плоскость 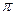. Выведем уравнение этой плоскости, т.е. уравнение, содержащее переменные х, у, z, которому удовлетворяют координаты любой точки, лежащей на плоскости 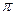и не удовлетворяют координаты никакой точки, не лежащейна этой плоскости.

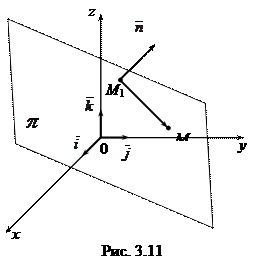
Пусть задана точка М ₁(х ₁, у ₁, z ₁) 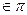и вектор 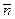= { А, В, C } перпендикулярный плоскости 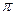(нормальный вектор плоскости). Пусть M (x, у, z) – произвольная точка, принадлежащая плоскости 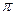. Тогда вектор

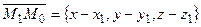
перпендикулярен вектору 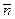(рис. 3.11), а поэтому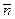 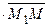= 0 (условие перпендикулярности векторов (см. разд. 2.4)) или

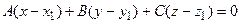. (3.11)

Итак, координаты любой точки М, лежащей в плоскости 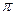, удовлетворяют этому уравнениюи, легко видеть, что координаты точки, не лежащей в плоскости 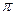, не удовлетворяют уравнению (3.11). Следовательно, уравнение (3.11) является уравнением плоскости и называется уравнением плоскости по точке и нормальному вектору.

Уравнение (3.11) является уравнением первой степени относительно текущих координат х, у, z. Можно показать (аналогично тому, как это было сделано в разд. 3.1), что всякое уравнение первой степени относительно x, у, z

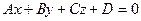(3.12)

является уравнением некоторой плоскости (оно называется общим уравнением плоскости), причем вектор 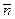= { А, В, C }, является нормальным вектором плоскости.

Если в уравнении (3.12) D = 0, то этому уравнению удовлетворяет тройка чисел (0, 0, 0), т.е. соответствующая плоскость проходит через начало координат. Нетрудно видеть, что плоскость 0 ху имеет уравнение 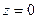, плоскость 0 xz – уравнение 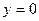, a плоскость 0 yz задается уравнением .

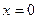Известно, что плоскость однозначно определяется тремя точками, не лежащими на одной прямой. Пусть 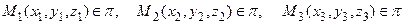и М (х, у, z) – произвольная точка плоскости 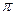(рис. 3.12). Рассмотрим векторы

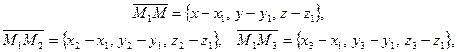
они компланарны, поэтомуих смешанное произведение равно 0, т.е.

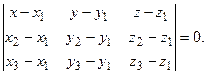(3.13)

Это уравнение называется уравнением плоскости по трем точкам.

Пусть плоскость 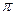пересекает оси координат в точках: М ₁(а, 0, 0), М ₂(0, b, 0), M ₃(0, 0, с). Подставляяих координаты в уравнение (3.13), находим:

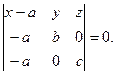
Вычислив определитель, получим:

,

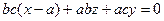откуда

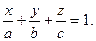
Это уравнение называется уравнением плоскости в отрезках.

Пример 3.4. Построить плоскость, заданную общим уравнением:

.

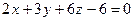Решение. Преобразуем данное уравнение в уравнение в отрезках

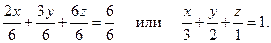
М ₁(3, 0, 0), М ₂(0 2, 0), М ₃(0, 0, 1).

По этим данным легко построить плоскость (рис. 3.13).