Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное расположение двух плоскостей в пространстве. Расстояние от точки до плоскости
|
|
Пусть плоскости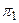 
и 
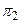заданы общими уравнениями:
, 
,
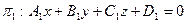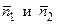– нормальные векторы этих плоскостей соответственно.
Плоскост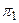и и 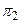параллельны или совпадают тогда и только тогда, когда векторы 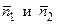коллинеарны. Записывая условие коллинеарности векторов (2.6), получаем: если 
то плоскости параллельны; если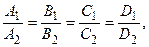 
то плоскости совпадают.
Если же координаты векторов 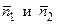не пропорциональны, то плоскости пересекаются по некоторой прямой l. Очевидно, что
.
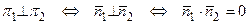Отсюда получаем условие перпендикулярности плоскостей
.
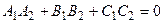Как и для двух прямых на плоскости можно вывести следующую формулу:
,
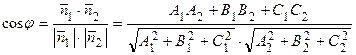где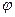 
– один из смежных двугранных углов между плоскостями. Расстояние d от точки М 0(х 0, у 0, z 0) до плоскости 
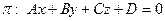вычисляется по формуле:
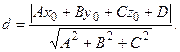
Пример 3.5. Составить уравнение плоскости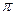 
, проходящей через точку
M 1(–1, 2, 5) параллельно плоскости :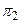 
.
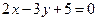Решение. Нормальный вектор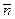 
={2, –3, 0} плоскости 
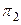является также нормальным вектором плоскости 
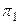. Используя равенство (3.11) получаем:
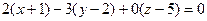
– уравнение плоскости 
по точке и нормальному вектору. Раскрывая скобки и приводя подобные слагаемые, найдем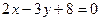 
– общее уравнение плоскости.