Уравнения прямой в пространстве

Прямую линию в пространстве можно задать как пересечение двух плоскостей. Рассмотрим систему двух уравнений:

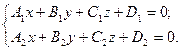. (3.14)

Каждое из уравнений определяет в пространстве плоскость. Если коэффициенты при переменных x, у, z не пропорциональны, то эти плоскости пересекаются по некоторой прямой l. Координаты любой точки удовлетворяют системе (З.14) тогда и только тогда, когда точка лежит на прямой l. Поэтому уравнения (3.14) являются уравнениями прямой l и называются общими уравнениями прямой.

Итак, прямая в пространстве задается двумя линейными уравнениями.

Выведем другие виды уравнений прямой в пространстве.

Пусть задана точка М ₁(х ₁, у ₁, z ₁), лежащая на прямой l и ее направляющий вектор 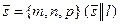. Пусть M (x, y, z) произвольная точка прямой l, тогда векторы 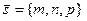и 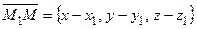коллинеарны и по формуле (2.6) получаем:

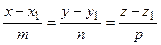(3.15)

– канонические уравнения прямой l (уравнения прямой по точке и направляющему вектору). Из канонических уравнений, введя параметр t (коэффициент пропорциональности), который может принимать любые действительные значения:

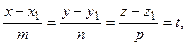
получаем параметрические уравнения прямой l:

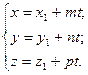
При изменении параметра t координаты точки М (х, у, z) изменяются и она перемещается по прямой l.

Заметим, что для прямой на плоскости можно вывести аналогичные параметрические уравнения:

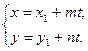
Уравнения прямой, проходящей через две заданные точки (уравнения прямой по двум точкам) М ₁(х ₁, у ₁, z ₁) и М ₂(х ₂, у ₂, z ₂), предлагается вывести самостоятельно, они имеет вид:

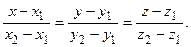
Рассмотрим переход от общих уравнений прямой к параметрическим.

Пусть прямая l задана уравнениями (3.14), т.е. является линией пересечения плоскосте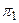й и 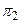, которые имеют нормальные векторы:

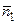= { A ₁, B ₁, C ₁} и 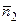= { A ₂, B ₂, C ₂}

(рис. 3.14). Запишем канонические уравнения прямой l. Для этого из системы (3.14) найдем одно решение (х ₁, у ₁, z ₁) – координаты точки М ₁(х ₁, у ₁, z ₁), лежащей на l (система (3.14) имеет бесконечное множество решений). Поскольку

,

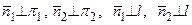поэтому вектор 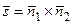параллелен прямой l, следовательно, – направляющий вектор l. Координаты вектора найдем по формуле (2.10), вычислив векторное произведение:

Подставив найденные числа в уравнения (3.15), получим канонические уравнения прямой l.

Пример 3.6. Прямая l является пересечением плоскостей:

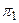: 2 х – у + z – 4 = 0 и 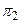: х + у – 2 z – 1 = 0.

Найти канонические уравнения прямой l.

Решение. 1) Решим систему уравнений:

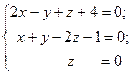
получим тройку чисел (–1, 2, 0) – точку пересечения прямой l с координатой плоскостью 0 ху.

2) Найдем направляющий вектор прямой l:

Подставляя полученные данные в уравнения (3.15), находим:

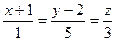
канонические уравнения прямой l.