
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гипербола. Гиперболойназывается множество точек на плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек
|
|
Гиперболой называется множество точек на плоскости, для каждой из которых абсолютная величина разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная (при условии, что эта величина меньше расстояния между фокусами и не равна 0).
Пусть F 1, F 2 – фокусы, расстояние между ними обозначим через 2 с, 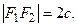
Выведем уравнение гиперболы. Для этого выберем прямоугольную декартову систему координат так, чтобы ось 0 х прошла через фокусы F 1, F 2 (рис. 3.19).
Тогда фокусы F 1, F 2 будут иметь координаты F 1(с, 0), F 2(– с, 0). Обозначим через М (х, у) произвольную точку гиперболы. По определению гиперболы 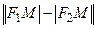 есть величина постоянная. Обозначим ее через 2 а (по условию 2 а < 2 с
есть величина постоянная. Обозначим ее через 2 а (по условию 2 а < 2 с 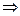 а < с).
а < с).
Подставляя в формулу: 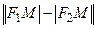 = 2 а вместо | F 1 M | и | F 2 M |их выражения через координаты получим:
= 2 а вместо | F 1 M | и | F 2 M |их выражения через координаты получим:

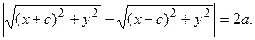
Избавимся от иррациональности так же, как делали в разд. 3.18 для эллипса, в итоге получим:
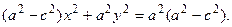
Поскольку 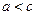 , то
, то 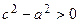 . Обозначим
. Обозначим 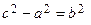 и подставим в предыдущее равенство:
и подставим в предыдущее равенство: 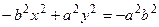 . Разделив обе части на
. Разделив обе части на 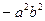 , имеем:
, имеем:
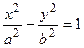 (3.19)
(3.19)
– каноническое уравнение гиперболы.
Исследуем свойства и начертим гиперболу, используя уравнение (3.19).
Четность степеней х и у в (3.19) указывает на то, что гипербола симметрична относительно осей 0 х, 0 у и начала координат.
Таким образом, гипербола имеет две оси симметрии, совпадающие в нашем случае с осями координат. В дальнейшем оси симметрии гиперболы будут называться осями гиперболы. Для нахождения точек пересечения с осью 0 х решим систему:
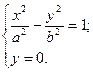
Получим: 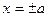 . Следовательно, гипербола пересекает ось 0 х в точках: А 1(а, 0), А 2(– а, 0), называемых вершинами гиперболы. Отрезок А 1 А 2 называется действительной осью, число а – действительной полуосью. Из системы
. Следовательно, гипербола пересекает ось 0 х в точках: А 1(а, 0), А 2(– а, 0), называемых вершинами гиперболы. Отрезок А 1 А 2 называется действительной осью, число а – действительной полуосью. Из системы
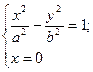
получаем: – у 2 = b 2 – противоречивое уравнение. Значит, гипербола не имеет пересечения с осью 0 у. Отрезок, соединяющий точки В 1(0, b), В 2(0, – b), называется мнимой осью, а число b – мнимой полуосью.
Рассмотрим часть гиперболы, расположенную в первой четверти. Для этого разрешим уравнение (3.19) относительно у, получим:
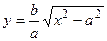 .
.
Для рассматриваемой части гиперболы х > а и при возрастании х от а до + 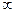 у возрастает от 0 до +
у возрастает от 0 до + 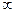 .
.
Введем вспомогательную прямую 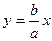 и сравним для одних и тех же значений аргумента х значения функции
и сравним для одних и тех же значений аргумента х значения функции 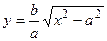 и значения ординаты взятой прямой
и значения ординаты взятой прямой 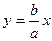 (ординату прямой обозначим Y, чтобы отличать от ординат точек гиперболы).
(ординату прямой обозначим Y, чтобы отличать от ординат точек гиперболы).
Очевидно, что 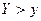 (если представить
(если представить 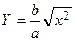 ), т.е. гипербола в первой четверти располагается ниже прямой
), т.е. гипербола в первой четверти располагается ниже прямой 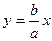 (рис. 3.20). Покажем, что при возрастании х гипербола приближается к прямой как угодно близко. Для этого вычислим разность
(рис. 3.20). Покажем, что при возрастании х гипербола приближается к прямой как угодно близко. Для этого вычислим разность 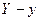 для одних и тех же значений переменной х:
для одних и тех же значений переменной х:
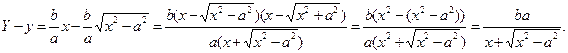
При неограниченном возрастании х знаменатель дроби неограниченно возрастает, а числитель остается постоянным, поэтому дробь стремится к 0 т.е. точки М 1(х, Y) и М 2(х, у) сближаются как угодно близко.
 |
Из симметрии гиперболы следует, что имеется еще одна прямая
 , к которой точки гиперболы приближаются неограниченно при стремлении х к –
, к которой точки гиперболы приближаются неограниченно при стремлении х к – 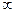 . Прямые
. Прямые 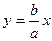 и
и  называются асимптотами гиперболы. Используя симметрию, строим гиперболы (рис. 3.21).
называются асимптотами гиперболы. Используя симметрию, строим гиперболы (рис. 3.21).
Практический совет. Преждечем строить гиперболу, постройте ее асимптоты.
Заметим, что уравнение 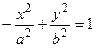 также задает гиперболу, у которой будут те же асимптоты
также задает гиперболу, у которой будут те же асимптоты 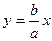 и
и  , но b – действительная полуось, а а – мнимая полуось, фокусы F 1 и F 2 лежат на оси 0 у.
, но b – действительная полуось, а а – мнимая полуось, фокусы F 1 и F 2 лежат на оси 0 у.
Отношение 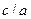 называется эксцентриситетом гиперболы и обозначается
называется эксцентриситетом гиперболы и обозначается 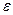 , т.е.
, т.е. 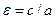 . Так как
. Так как 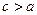 , то
, то 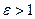 . Из формулы
. Из формулы 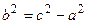 имеем:
имеем: 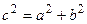 ,
,
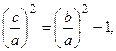 т.е.
т.е. 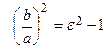 .
.
Следовательно, эксцентриситет характеризует форму гиперболы.
При 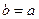 (
(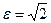 ) имеем равнобочную гиперболу, уравнение которой:
) имеем равнобочную гиперболу, уравнение которой: 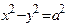 .
.
Рассмотрим график функции 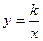 (или кривую второго порядка
(или кривую второго порядка 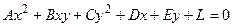 при А = С = D = Е = 0). Перейдем к новым координатам X, Y путем поворота системы координат 0 ху на угол
при А = С = D = Е = 0). Перейдем к новым координатам X, Y путем поворота системы координат 0 ху на угол 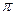 /4, получим формулы перехода:
/4, получим формулы перехода:
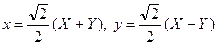 .
.
Подставим эти х, у в уравнение ху = k:
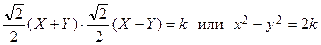 .
.
Таким образом, 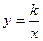 является равнобочной гиперболой, действительная полуось которой при k < 0 лежит на оси 0 Y (рис. 3.22), при k > 0 – на оси 0 X (рис. 3.23) в новой системе координат 0 XY.
является равнобочной гиперболой, действительная полуось которой при k < 0 лежит на оси 0 Y (рис. 3.22), при k > 0 – на оси 0 X (рис. 3.23) в новой системе координат 0 XY.

Если в уравнении второго порядка: 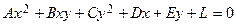 коэффициенты В = 0, А и С – разных знаков, то после выделения полных квадратов получим уравнение:
коэффициенты В = 0, А и С – разных знаков, то после выделения полных квадратов получим уравнение: 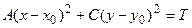 . При Т
. При Т 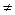 0 получаем гиперболу, при Т = 0 – пару прямых. Например, при А = 1, С = –l, Т = 0 имеем:
0 получаем гиперболу, при Т = 0 – пару прямых. Например, при А = 1, С = –l, Т = 0 имеем:
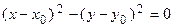 ,
,
отсюда
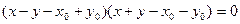 .
.
Следовательно, уравнение
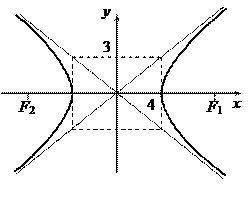
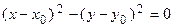
задает две прямые:
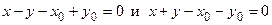 .
.
Пример 3.9. Составить каноническое уравнение гиперболы, если расстояние между ее вершинами равно 8, а между фокусами – 10. Сделать чертеж.
Решение. 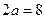 ,
, 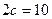 , отсюда
, отсюда 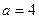 ,
, 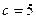 .
.
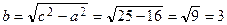 .
.
Проведем асимптоты: 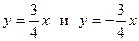 и построим ветви гиперболы (рис. 3.24).
и построим ветви гиперболы (рис. 3.24).