Решения задач

4.1. Исследование и решение систем линейных
уравнений

Дана система линейных уравнений

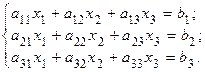(4.1)

Доказать ее совместность и решить: 1) методом Гаусса; 2) средствами матричного исчисления.

Доказать совместность – это значит доказать, что данная система имеет хотя бы одно решение. При доказательстве совместности системы (4.1) может быть использована теорема (1.2) Кронекера-Капелли.

В рассматриваемом случае

, ,

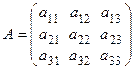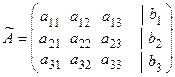требуется доказать, что rang A = rang .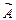

Для вычисления ранга матрицы может быть использован метод окаймляющих миноров. Минор 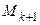порядка k + 1, содержащий в себе минор 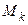порядка k, называется окаймляющим минором .

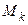Если у матрицы A существует минор 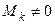, а все окаймляющие его миноры 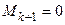, то r (A) = k.

В случае если число уравнений системы совпадает с числом неизвестных, для доказательства совместности можно воспользоваться теоремой (1.1) Крамера.

1) Применение метода Гаусса для решения систем трех линейных уравнений заключается в последовательном исключении неизвестных в уравнениях системы (4.1) с целью приведения ее к треугольному виду:

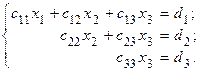(4.2)

При этом допускаются следующие элементарные преобразования системы, приводящие к эквивалентным системам уравнений:

а) перестановка уравнений в системе;

б) умножение обеих частей уравнений на одно и то же число неравное нулю;

в) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на одно и то же число;

г) исключение уравнений вида 0 = 0.

В полученной системе (4.2), из 3-го уравнения вычисляется 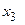и его значение подставляется во 2-е уравнение, затем из 2-го уравнения вычисляется 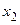и подставляется вместе с 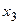в 1-е уравнение, после чего из 1-го уравнения вычисляется .

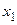2) Для решения систем линейных уравнений средствами матричного исчисления необходимо:

а) вычислить определитель 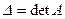матрицы данной системы и убедиться, что 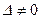. Если 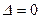, то матричный метод не применим;

б) найти матрицу 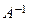, обратную к матрице A, по формуле:

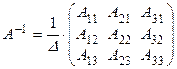, (4.3)

где 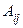– алгебраические дополнения элементов 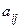матрицы A (в нашем случае
i, j = 1, 2, 3). Напомним, что алгебраическое дополнение 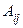равно определителю, полученному из элементов матрицы A после вычеркивания i -й строки и j -го столбца этой матрицы, умноженному на коэффициент, равный ;

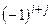в) найти решение системы по формуле: .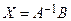

Пример. Дана система линейных уравнений

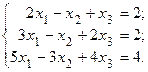
Доказать ее совместность и решить: 1) методом Гаусса; 2) средствами матричного исчисления.

Решение. Докажем совместность. Запишем расширенную матрицу системы

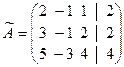
и найдем ее ранг. Элемент матрицы 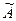, стоящий в левом верхнем углу, отличен от нуля, следовательно, 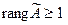. Среди миноров второго порядка, окаймляющих (включающих в себя) этот элемент, также есть отличные от нуля, например:

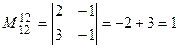, т.е. .

Из миноров третьего порядка, окаймляющих 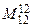, возьмем минор :

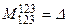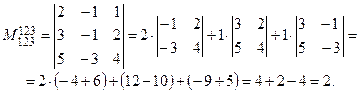
Так как 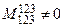, то 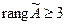, а так как у матрицы 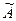миноров 4-го порядка не существует, то 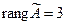. Так как 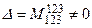, то и 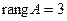. Таким образом, 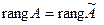, и совместность доказана.

1) Применим метод Гаусса к решению данной системы.

Шаг 1. Умножим первое уравнение системы на 1/2, чтобы коэффициент при x ₁ стал равен единице.

Шаг 2. Члены первого уравнения, во-первых, умножим на –3 и прибавим к членам второго уравнения, во-вторых, умножим на –5 и прибавим к членам третьего уравнения. В результате получим систему:

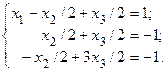
Шаг 3. К членам третьего уравнения прибавим члены второго уравнения. В результате, получим:

.

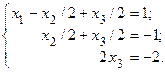Таким образом, исходная система приведена к эквивалентной системе треугольного вида. Как известно, она имеет единственное решение. Решаем эту систему, начиная с последнего уравнения:

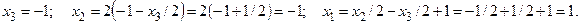
Ответ: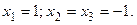

2) Применяем матричный метод к решению системы. Формируем матрицы, состоящие из элементов системы:

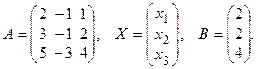
а) Определитель системы 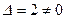, значит, матричный метод применим.

б) Запишем систему в матричном виде :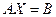

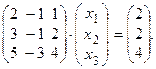
в) Вычисляем алгебраические дополнения :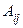

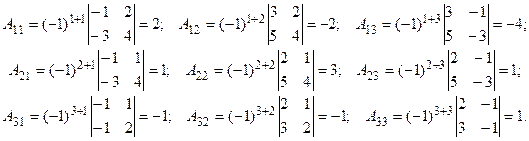
Подставляя найденные значения 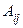в формулу (4.3), получим:

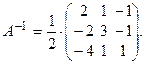
г) Воспользуемся формуло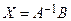й или

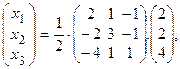
получим: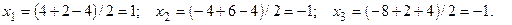

Ответ: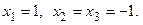

4.2. Определение координат вектора относительно
заданного базиса

Пример. Даны векторы: 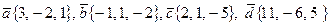в некотором базисе. Показать, что векторы 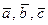образуют базис, и найти координаты вектора 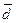в этом базисе.

Решение. Составим определитель D из координат векторов 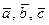и вычислим его разложением, например, по первой строке:

.

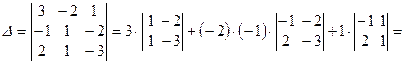
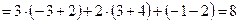Так как D ¹ 0, то векторы 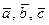образуют базис (см. разд. 1.9).

Найдем координаты вектора 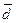относительно базиса 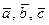, т.е. числовые коэффициенты a ₁ , a ₂ , a ₃ разложения

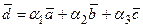
или

.

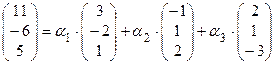В силу определения равенства векторов и определения операций сложения векторов и умножения вектора на число, когда известны координаты векторов относительно некоторого базиса, последнее векторное равенство можно записать в виде системы трех линейных уравнений с тремя неизвестными:

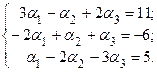
Решая эту систему, например, по формулам Крамера, находим:

a ₁ = 2, a ₂ = 3, a ₃ = 1.

Ответ: 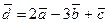.