Прямая на плоскости

Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и 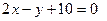и уравнение одной из его диагоналей: .

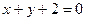Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой 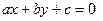определяется по формуле:

.

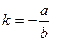Стороны параллельны, так как имеют одинаковый угловой коэффициент:

.

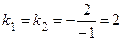Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:

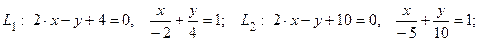
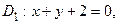
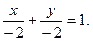
Наметим план решения:

1) находим вершины ромба P и Q;

2) находим точку пересечения диагоналей ромба N;

3) через точку N проводим диагональ D ₂;

4) находим оставшиеся вершины ромба R и S.

1) Так как точка P является точкой пересечения прямых L ₂ и D ₁, то ее координаты находим из системы уравнений:

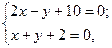
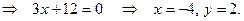
Из рис. 4.1 сразу находим координаты точки Q (–2, 0). 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка 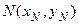является серединой отрезка PQ, поэтому ее координаты – полусумма соответствующих координат точек P и Q:

.

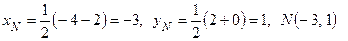3) Так как диагонали ромба взаимно перпендикулярны, то прямая D ₂ перпендикулярна вектору 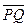. Найдем его координаты:

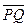= {–2 – (–4); 0 – 2} = {2; –2}.

По формуле (3.1) находим уравнение диагонали D ₂ как уравнение прямой, проходящей через точку N (–3, 1) перпендикулярно вектору 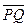= {2; –2}:

2× (x – (–3)) + (–2)(y – 1) = 0, x – y + 4 = 0.

4) Вершины ромба R и S – точки пересечения прямых L ₂ и D ₂, L ₁ и D ₂, соответственно, находим из уравнений:

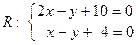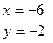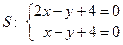, Þ , , Þ .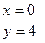

Ответ: P (–4, 2) R (–6, –2), Q (–2, 0), S (0, 4).

Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, –7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин.

Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:

h: 3 x + y + 11 = 0,

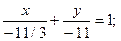
m: x + 2 y + 7 = 0,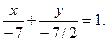

План решения:

1) находим уравнение прямой PQ;

2) находим координаты точки R;

3) находим уравнения прямых RP и RQ.

1) Находим нормальный вектор прямой h: 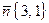. Уравнение стороны PQ, проходящей через точку P (2, –7) параллельно вектору 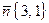, запишем в виде:

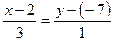, x – 3 y – 23 = 0.

Находим координаты точки Q – точки пересечения прямых PQ и m:

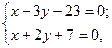x = 5, y = – 6.

2) По свойству медианы треугольника PQR точка S (x_S, y_S) является серединой отрезка RP. Следовательно:

, .

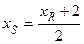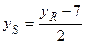Точка S лежит на медиане m, значит,

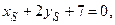
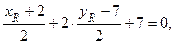
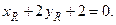
Точка R лежит на высоте h, значит,

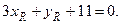
Из последних двух уравнений определяем координаты точки R, решая систему:

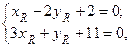
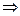
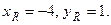
3) Используя формулу (3.4), составим уравнение прямой RP, проходящей через две заданные точки R и P:

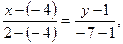
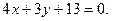
Аналогично, составим уравнение прямой RQ:

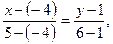
Ответ: x – 3 y – 23 = 0, ,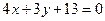

4.4. Вывод уравнения линии, определенной
как геометрическое место точек.
Кривые второго порядка

Пример. Составить уравнение линии, расстояния каждой точки которой от точки A (0, –2) и от прямой 2 y – 5 = 0 относятся как 4: 5.

Решение. Возьмем произвольную точку M (x, y), которая принадлежит искомой линии. Расстояние d между точками A и M равно:

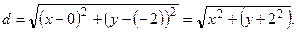
Расстояние от точки M до прямой 2 y – 5 = 0 находим по формуле (3.10):

По условию 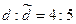, следовательно, 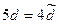, т.е.

.

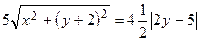Возведем обе части уравнения в квадрат:

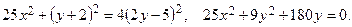
Получили уравнение кривой второго порядка. Для более детального исследования выделим полные квадраты:

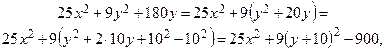
следовательно,

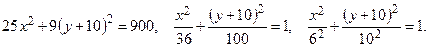
Теперь видно, что искомая линия – эллипс, полученный параллельным смещением эллипса:

вдоль оси 0 y на 10 единиц вниз.

Ответ: эллипс