Парабола

Параболой называется множество точек на плоскости, для каждой из которых расстояние до данной точки (называемой фокусом) равно расстоянию до данной прямой (называемой директрисой).

Пусть F – фокус, l – директриса параболы, р – расстояние от фокуса F до директрисы l (назовем р параметром параболы). Выведем уравнение параболы.

Выберем ось 0 х так, чтобы она проходила через фокус F перпендикулярно l, а начало системы координат расположим в середине перпендикуляра, опущенного из F на l (рис. 3.25). Тогда фокус имеет координаты F (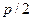, 0), а директриса описывается уравнением .

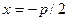Пусть М (х, у) – произвольная точка параболы, тогда по определению параболы расстояние MN от М до l равно расстоянию MF от М до фокуса (MN = MF):

, .

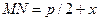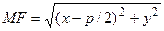Возведя обе части этого уравнения в квадрат, получим: 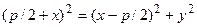. После упрощения найдем:

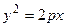(3.20)

– каноническое уравнение параболы.

По уравнению (3.20) исследуем свойства параболы и начертим ее. Из четности степени у в (3.20) следует, что парабола симметрична относительно оси 0 х. Парабола проходит через начало координат, так как х = 0 и у = 0 удовлетворяют уравнению (3.20). Далее, х 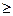0 (так как р > 0), поэтому парабола лежит правееоси 0 у. В первой четверти парабола задана равенством 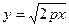, откуда видим, что с возрастанием х возрастает и у. Используя симметричность параболы, изображаем её (рис. 3.26).

Заметим, что уравнение 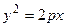при отрицательном р также задает параболу, которая будет расположена слева от оси 0 у (рис. 3.27). Уравнение 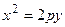описывает параболу, симметричную относительно оси 0 у, лежащую выше оси 0 х при р > 0 и лежащую ниже оси 0 х при р < 0.

Пример 3.10. Найти уравнение параболы, которая симметрична относительно оси 0 х, проходит через начало координат и точку М (1, –4).

Решение. Уравнение этой параболы имеет вид 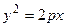, надо найти только параметр р. Координаты точки М (1, –4) удовлетворяют этому уравнению, поэтому

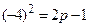, откуда 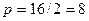. Получаем 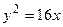– уравнение искомой параболы.

Рассмотрим общее уравнение второго порядка:

.

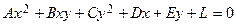Если В = 0, С = 0 и Е 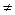0, то

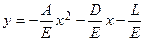. (3.21)

Получили квадратичную функцию (квадратный трехчлен), перейдем к обычным обозначениям: 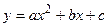. Из школьного курса математики известно, что графиком квадратного трехчлена (3.21) является парабола с вершиной в точке М ₀(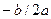, 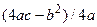), с осью симметрии, параллельной оси 0 у (выясняется это с помощью выделения полного квадрата).