Кривые второго порядка. Окружность

Пусть на плоскости задана прямоугольная система координат 0 ху.

Кривой второго порядка называется линия на плоскости, определяемая уравнением второй степени относительно текущих координат точки М (х, у, z). В общем случае это уравнение имеет вид:

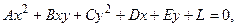(3.17)

где коэффициенты А, В, С, D, E, L – любые действительные числа, причем хотя бы одно из чисел А, B, С отлично от нуля.

В дальнейшем будут рассмотрены четыре вида кривых второго порядка: окружность, эллипс, гипербола и парабола.

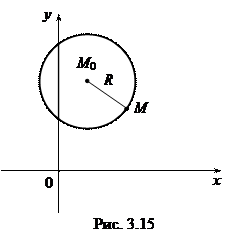
Окружностью называется множество точек на плоскости, расстояние от которых до фиксированной точки М ₀(х ₀, у ₀) постоянно и равно R. Точка М ₀ называется центром окружности, а число R – ее радиусом (рис. 3.15).

Получим уравнение окружности. Пусть М (х, у) есть произвольная точка окружности. Тогда по определению | M ₀ М | = R или

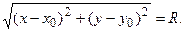
Возводя обе части равенства в квадрат, получим:

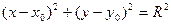
– уравнение окружности с центром в точке М ₀(х ₀, у ₀) и радиусом R.

Если центр окружности совпадает с началом координат, то имеем:

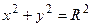
– каноническое уравнение окружности.

Рассмотрим уравнение (3.17) при условии А = С 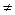0, В = 0. После деления этого уравнения на А и переобозначения коэффициентов получим уравнение:

.

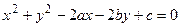Выделим в нем полные квадраты 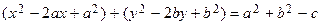или .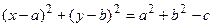

Если 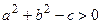, то обозначив 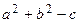через R ², получим уравнение окружности: 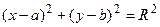с центром в точке М ₀(а, b) радиуса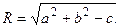

Если 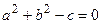, то уравнение: 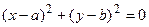задает только точку М ₀(а, b).

Если 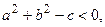то никакого геометрического образа нет.

Эллипс

Эллипсом называется множество точек на плоскости, для каждой из которых сумма расстояний до двух данных точек есть величина постоянная (причем эта величина больше расстояний между данными точками). Данные точки называются фокусами эллипса.

Обозначим фокусы F ₁, F ₂ и расстояние между ними через 2 с, т.е. 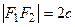. Выберем декартову систему координат так, чтобы ось 0 х прошла через фокусы, а начало координат совпадало с серединой отрезка F ₁ F ₂, (рис. 3.16). Тогда фокусы будут иметь координаты F ₁(с, 0), F ₂(– с, 0). Обозначим через М (х, у) произвольную точку эллипса. По определению эллипса сумма расстояний 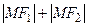есть величина постоянная, обозначим ее через 2 а (по условию 2 а > 2 с, т.е. а > с). В равенстве:

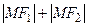= 2 а

выразим расстояния через координаты точки М, получим:

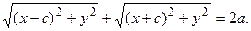
Чтобы избавиться от иррациональностей, перенесем один из радикалов в правую часть равенства и возведем обе части в квадрат:

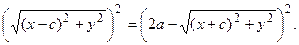
После очевидных преобразований получим:

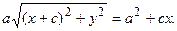
Возведем еще раз это равенство в квадрат и упростим:

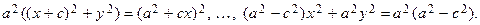
Разделим обе части равенства на :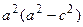

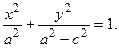
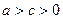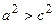Поскольку , то и 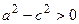. Пусть 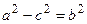, тогда из последнего равенства получим:

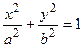(3.18)

– каноническое уравнение эллипса.

Установим форму эллипса, используя его уравнение. В каноническом уравнении (3.18) текущие координаты х, у входят лишь в четных степенях, следовательно, эллипс симметричен относительно осей 0 х, 0 у и начала координат. Оси симметрии эллипса называются его осями, точка пересечения осей – центром эллипса.

Найдем точки пересечения эллипса с осями координат. Решая совместно систему уравнений

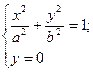
получим: 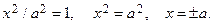Следовательно, с осью 0 х эллипс пересекается в точках А ₁(а, 0), А ₂(– а, 0). Аналогично находим, чтоэллипс пересекается с осью 0 у в точках В ₁(0, b), В ₂(0, – b). Найденные точки называется вершинами эллипса, отрезки А ₁ А ₂, В ₁ В ₂ – большой и малой осями соответственно.

Определим форму эллипса в первой четверти, для этого разрешим уравнение эллипса (3.18 ) относительно переменной у:

.

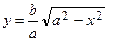Отсюда для первой четвертиимеем 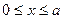. При возрастании х от 0 до а переменная у уменьшается от b до 0. Воспользовавшись симметрией эллипса, изобразим его полностью (рис. 3.17).

Заметим, что уравнение 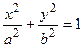при 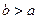также задает эллипс, только его фокусы будут расположены на оси 0 у и поэтому b – большая полуось, а – малая полуось.

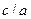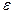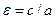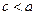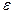Отношение называется эксцентриситетом эллипса и обозначается: , . Так как , то < 1.

Эксцентриситет характеризует форму эллипса. Из формулы 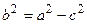получаем:

.

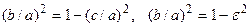Следовательно, с уменьшением 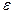отношение 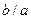стремится к 1, т.е. b мало отличается от а и форма эллипса становится ближе к форме окружности. В предельном случае при 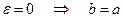, получается окружность, уравнение которой есть

х ² + у ² = а ².

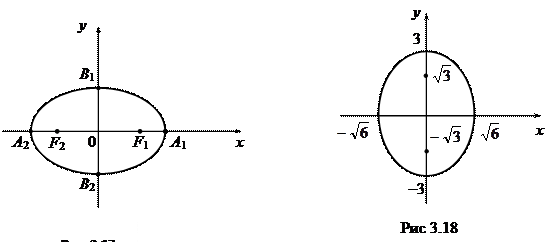
Пример 3.8. Построить кривую:

9 х ² + 6 у ² = 54.

Решение. Разделим обе части уравнения на 54, получим:

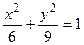
– каноническое уравнение эллипса с малой полуосью а = 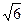и большой полуосью b = 3. Фокусы эллипса лежатна оси 0 у. В этом случае 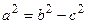, следовательно, 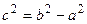, т.е. с = 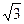. Фокусы эллипса имеют координаты F ₁(0, 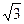), F ₂(0, – 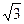) (рис. 3.18).