Условный экстремум. Метод множителей Лагранжа.

Условным экстремумом функции z=f(x, y) в точке M0(x0; y0) называется экстремум этой функции, достигнутый при условии, что переменные x и y в окрестности данной точки удовлетворяют уравнению связи φ (x, y)=0. Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие φ (x, y)=0.

Метод множителей Лагранжа, метод нахождения условного экстремума функции 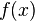, где 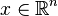, относительно 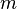ограничений 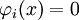, где 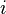меняется от единицы до .

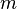1)Составим функцию Лагранжа в виде линейной комбинации функции 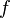и функций 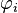, взятых с коэффициентами, называемыми множителями Лагранжа — :

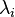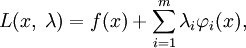
где .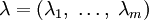

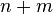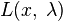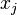2)Составим систему из уравнений, приравняв к нулю частные производные функции Лагранжа по и .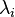

3)Если полученная система имеет решение относительно параметров 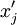и 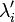, тогда точка 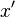может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.