
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах.
|
|
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U:
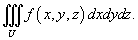
Тогда формула замены переменных в тройном интеграле записывается в виде:
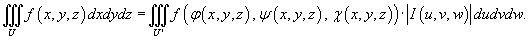
В приведенном выражении 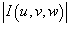 означает абсолютное значение якобиана.
означает абсолютное значение якобиана.
(Якобиан-определитель матрицы Якоби).
Сферическими координатами точки M(x, y, z) называются три числа − ρ, φ, θ, где
ρ − длина радиуса-вектора точки M;
φ − угол, образованный проекцией радиуса-вектора на плоскость Oxy и осью Ox;
θ − угол отклонения радиуса-вектора от положительного направления оси Oz (рисунок 1).
Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования U представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет вид f (x2 + y2 + z2).
В цилиндрических координатах положение точки M(x, y, z) в пространстве Oxyz определяется тремя числами − ρ, φ, z, где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz